Chaotyczne ruchy cząstek - część 2. Ruchy Browna

Omówione w poprzedniej części zjawisko dyfuzji dotyczyło sytuacji, w której rozmiary cząsteczek dwóch substancji są porównywalne. W przybliżeniu możemy traktować takie cząsteczki jak zderzające się sprężyście kule. W trakcie zderzenia następuje między nimi przekaz energii i pędu, co manifestuje się zmianą wartości ich prędkości oraz kierunku ruchu. Przy znacznej liczbie cząsteczek obu rodzajów i w sytuacji, w której zderzenia zachodzą relatywnie często, stężenia substancji stopniowo się wyrównują. Cząsteczka, która pierwotnie była w określonym punkcie przestrzeni, może znaleźć się po kilku zderzeniach w bardzo odległym miejscu.

A jeśli zmienimy wielkość cząsteczki?

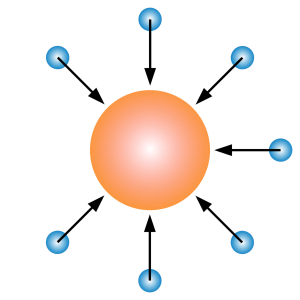
Warto zadać sobie pytanie, czy podobne zjawisko zaobserwujemy również w przypadku znacznej dysproporcji wielkości cząsteczek. Dla uproszczenia ograniczmy rozważanie do jednej dużej cząsteczki otoczonej licznymi cząsteczkami o znacznie mniejszej średnicy. Teoretycznie duża cząsteczka jest bombardowana ze wszystkich stron z jednakowym prawdopodobieństwem przez mniejsze cząsteczki. Całkowity przekaz pędu wynosi w takiej sytuacji zero, zatem duża cząsteczka nie powinna zmieniać swojego położenia. Czy jednak tak się dzieje w rzeczywistości?

1. Gdyby w każdej chwili pyłek był bombardowany z każdej strony przez dokładnie taką samą liczbę cząsteczek wody, całkowity przekaz pędu byłby zerowy. Pyłek nie poruszałby się

2. Nawet niewielkie ﬂuktuacje gęstości wody mogą spowodować, że w danej chwili przekaz pędu będzie niezerowy. W efekcie pyłek uzyska prędkość i wykona ruch

Odrobina historii

W 1827 roku Robert Brown zaobserwował chaotyczne ruchy pyłków kwiatowych w zawiesinie wodnej. Początkowo próbowano je tłumaczyć na gruncie biologii, doszukując się w tym zjawisku nieznanej wcześniej zdolności pyłków do wykonywania aktywnego ruchu. Zakładano bowiem, że ruchliwość pyłku w środowisku wilgotnym mogła być w jakiś sposób korzystna dla roślin, potencjalnie zwiększając ich szanse na zapylenie.

Teoria ta szybko upadła, ponieważ w identyczny sposób poruszały się inne cząsteczki, zarówno pochodzenia organicznego, jak i nieorganicznego. Niektóre z tych substancji nie miały żadnych funkcji biologicznych. Ruchy tego samego rodzaju można było zaobserwować w przypadku zawiesin tłuszczu w roztworach wodnych czy drobin pigmentu w różnych rozpuszczalnikach. Z obserwacji wynikało, że intensywność ruchów rośnie wraz z temperaturą i maleje wraz z wielkością cząsteczki.

Na rozwiązanie zagadki trzeba było poczekać dobrych kilka dekad. Dopiero w roku 1906 pełne wyjaśnienie tego zjawiska podał Marian Smoluchowski, a rok wcześniej swoją propozycję opublikował Albert Einstein. Obaj naukowcy rozumieli, że ruchy Browna są skutkiem uderzeń cząsteczek wody w większą drobinę materii. Jednak pełne wyjaśnienie podał Smoluchowski, słusznie zauważając, iż należy posłużyć się rachunkiem prawdopodobieństwa, nie skupiając się na analizie pojedynczych zderzeń.

Ponieważ w każdym ośrodku mogą powstawać lokalne fluktuacje gęstości, cząstka pyłku zawieszona w wodzie może otrzymać w danej chwili niezerowy przekaz pędu i wykonać ruch w określonym kierunku. W kolejnej chwili zagęszczenia i rozrzedzenia ośrodka mogą się utworzyć w zupełnie innych miejscach i pyłek poruszy się w inną stronę. W efekcie zaobserwujemy jego chaotyczne ruchy.

Zadanie

W jakim kierunku będzie skierowany wektor pędu pyłku przedstawionego na drugim rysunku? Wskaż prawidłową odpowiedź.

A. w prawo,
B. w lewo,
C. w górę,
D. w dół

Symulacja ruchów Browna

Symulację ruchów Browna można przeprowadzić za pomocą prostej gry losowej. Potrzebna będzie plansza (może być do szachów), żeton i kostka ośmiościenna. Taką kostkę bez trudu można zakupić w sklepach oferujących akcesoria do gier strategicznych. Można również wykorzystać kostkę sześcienną, ale w takiej sytuacji należy samodzielnie wykonać odpowiednią planszę według wzoru z rysunku 3.

3. Fragment planszy do gry kostką ośmiościenną (strona lewa) lub sześcienną (strona prawa).
Na rysunku zaznaczono propozycję sposobu przesuwania żetonu po wyrzuceniu odpowiedniej
liczby oczek. W następnym ruchu pole, na którym aktualnie leży żeton,
staje się nowym polem startowym

Żeton, symbolizujący dużą cząstkę, ustawiamy na polu znajdującym się w centralnej części planszy. Za pomocą kostki losujemy kierunek, w którym nastąpi przekaz pędu. Żeton przesuwamy zgodnie z wylosowanym kierunkiem na jedno z pól bezpośrednio sąsiadujących z polem startowym. Po każdym ruchu notujemy aktualne położenie cząstki lub fotografujemy planszę.

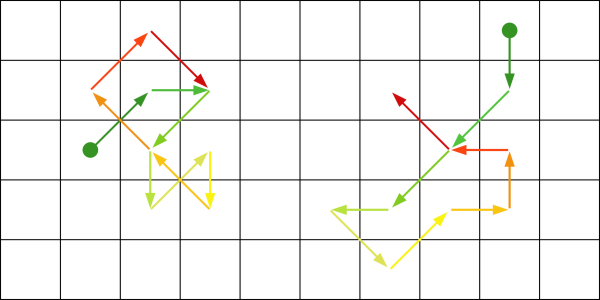
Żeby zobrazować ruchy Browna, wystarczy zazwyczaj dziesięć do kilkunastu rzutów kostką. Ponieważ gra jest bardzo prosta, ćwiczenie można wykonywać w podziale na grupy. Uczniowie uzyskają wówczas swoje indywidualne wyniki, które będą mogli porównać i omówić. Poniżej zostały przedstawione przykładowe wyniki dwukrotnego wykonania opisanej symulacji.

Uczniów zainteresowanych grafiką komputerową lub programowaniem warto zachęcić do zmontowania animacji poklatkowej obrazującej ruch cząstki lub napisania prostego programu symulacyjnego.

4. Przykładowe wyniki gry symulacyjnej. Dla lepszej czytelności rysunku kolor strzałek
symbolizujących ruch cząstki zmienia się od zielonego do czerwonego.
Zielona kropka oznacza punkt startowy symulacji

Dla nauczyciela

Materiał z niniejszego artykułu można wykorzystać na lekcjach fizyki do realizacji poniższych punktów podstawy programowej.

Szkoła ponadpodstawowa, zakres rozszerzony

VI. Termodynamika. Uczeń:

11. opisuje związek pomiędzy temperaturą w skali Kelvina a średnią energią ruchu cząsteczek i energią wewnętrzną gazu doskonałego;
18. opisuje zjawisko dyfuzji; posługuje się pojęciem fluktuacji, opisuje ruchy Browna.

Joanna Borgensztajn

Przeczytaj także:

Chaotyczne ruchy cząstek - część 1. Dyfuzja