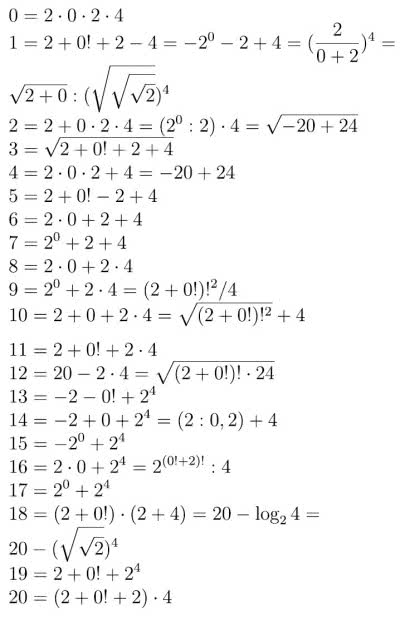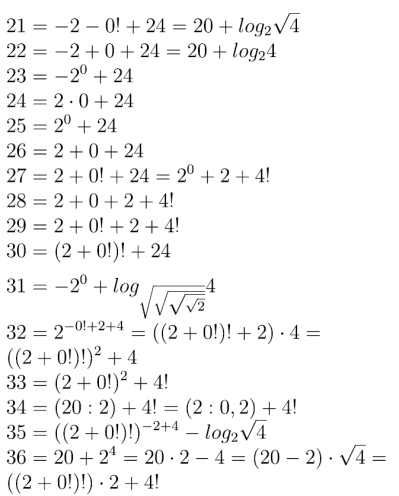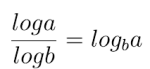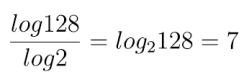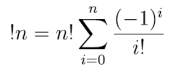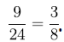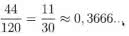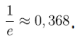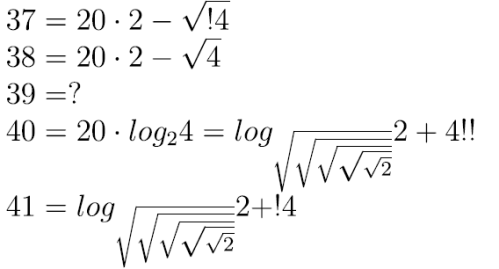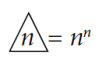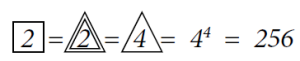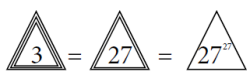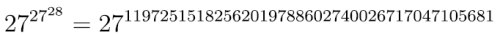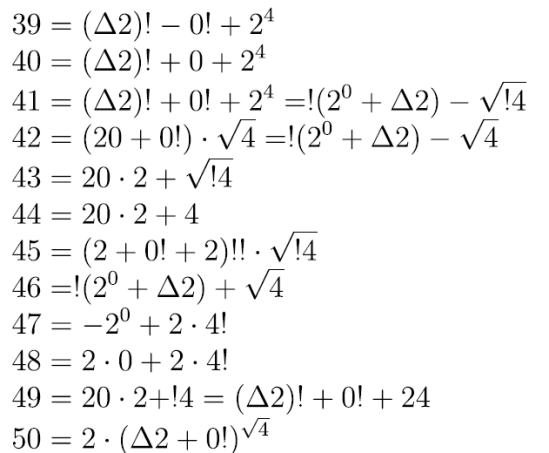Arytmetyka z morałem

Zastanowiłem się, co odpowiedzieć. Czy zaprezentować się jako platonik, czy arystotelik? Być bardziej Leibnizem czy Kartezjuszem? Czy liczby są wymyślone przez ludzi, czy istnieją niezależnie od nas. To średniowieczny spór o uniwersalia. Zaczyna się od Sokratesa. Jeżeli stwierdzamy, że dwa kawałki drewna są równe, to musimy mieć w umyśle zakodowaną jakąś ideę równości. Czy istnieje ona niezależnie od nas?

Postanowiłem zachować się jak blondynka z serii prymitywnych dowcipów: „skąd mam wiedzieć, co myślę, póki nie usłyszę, co mówię?” Nie pamiętam już dokładnie, co mówiłem Marcie. Nie będę do tego wracał, bo… ten odcinek „Rozmaitości Matematycznych” pisałem na początku stycznia, kiedy obecny rok był jeszcze noworodkiem i jak my wszyscy, byłem pełny nadziei, że najgorsze minęło. Wraz z kolegą z Krakowa przerzucaliśmy się ciekawostkami liczbowymi. Takie kurioza nie są poważną matematyką. Można powiedzieć, że w ogóle nie są matematyką. W matematyce dążymy do odkrywania ogólnych prawd, twierdzeń, własności liczb, figur i funkcji. Pojedyncze wymyślne własności to tylko łamigłówki. Nie każda łamigłówka jest matematyką, chociaż przecież nad niektórymi trzeba się mocno pogłowić. Wiedział już to Sherlock Holmes, choć jego matematyczna wiedza była zapewne znikoma.

Dodatkową zachętą do wyboru takiego tematu był list od Czytelnika, zresztą mojego dawnego znajomego. Pytał on o cechy podzielności przez różne liczby. Odpowiedzią zajmę się może w następnym odcinku. Dziś będzie trochę zabaw liczbowych, ale łagodnie przejdziemy do matematyki z wyższej półki.

Jak wiadomo, nowe dziedziczy po starym: dzieci po rodzicach, niekiedy trafi się i bogaty bezdzietny wujek milioner. Oczywiście lepiej, żeby wszystko działało w naturalnym kierunku, bo to bardzo przykre, gdy rodzice dziedziczą po dzieciach. Wspomniany kolega z Krakowa przysłał mi przykład dziedziczenia w świecie liczb. Co nowy rok ma ze starego?

2024 = 5 · 3 · (2³) · (2 + 3 + 2³)

Odpowiedziałem przykładem, który rozwinę pod koniec bieżącego roku:

2025 = (24 + 2⁴ + (2/4) · 2 + 4)^-2+4

a nawet przygotowałem sobie grunt pod kolejnego sylwestra. Na pewno da się prościej, ale  

Wykrzyknik oznacza ważną i znaną na pewno wielu Czytelnikom funkcję „silnia” - to iloczyn kolejnych liczb naturalnych: 1!=1, 2!=1∙2=2, 3!=1∙2∙3=6, 4!=1∙2∙3∙4=24 i tak dalej. Wartości tej funkcji rosną bardzo szybko i trudno je nawet przedstawić na wykresie.

Dla naszej zabawy z liczbami ważna będzie wartość 0!, silnia liczby zero. Przyjmuje się, że jest to równe 1. Można powiedzieć, że jest to tylko umowa, ale można odnieść się do wiadomości licealnych. Wartość n! to liczba możliwych ustawień n liczb (permutacji). Dwie liczby mogę ustawić na dwa sposoby: 1 2 albo 2 1. Jeżeli jest tylko jedna liczba, to nietrudno się zgodzić, że jest jedno ustawienie. A jeżeli liczb w ogóle nie ma? To trochę pozamatematyczne rozumowanie, ale też się można zgodzić, że zbiór pusty można uporządkować tylko na jeden sposób: nic z nim nie robić. Piszę o tym również dlatego, że jest to częsty błąd uczniów i studentów: silnia zera nie jest zerem, tylko 1.

Pobawmy się zatem liczbami. 

Reguły są chyba jasne. Należy wyrazić kolejne liczby naturalne za pomocą cyfr 2,0 2,4, użytych w tej kolejności i połączonych dowolnymi działaniami arytmetycznymi, w tym łączenia cyfr w liczby. Właśnie niesprecyzowanie, jakie mogą być te działania, powoduje, że jest to tylko zabawa.

***

Wykorzystajmy jednak pomysł z liczbą 31 do wykazania, że

Każdą liczbę naturalną można otrzymać z cyfr 2, 0, 2, 4, użytych tylko raz i w tej właśnie kolejności. Wolno używać wszelkich działań.

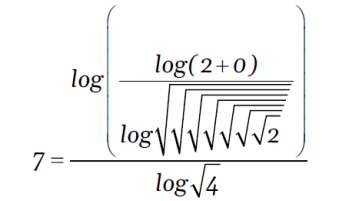
Sposób nieco karkołomny, mogący przyprawić wszystkich o ból głowy, nawet jeżeli logarytmy dobrze opanowaliśmy. Ale jest to tak zwane „dobre ćwiczenie” dla licealistów, zmagających się z logarytmami. Pokażę na przykładzie liczby 7. Otóż 

Wygląda przerażająco. Jak to często się zdarza: nie taki diabeł straszny, jak go malują. Sprawdzajmy.
Zacznijmy od liczby

Mamy w mianowniku pod logarytmem siedem znaków pierwiastka, czyli jest to pierwiastek z 2, stopnia 128. 

Pamiętamy, że

a zatem nasze x to logarytm liczby 2 przy podstawie

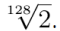
A ja wspomnę dawno minione lata szkolne. Musieliśmy recytować formułkę: logarytm liczby a przy podstawie p jest to wykładnik potęgi, do której należy podnieść podstawę, żeby otrzymać liczbę logarytmowaną a.

Teraz to się przydaje. Uczenie się na pamięć ma nie tylko wady. Ma i zalety. Z samego określenia logarytmu widzimy więc, że x=128. Oczywiście √4 = log2. I znów przypominamy sobie iloraz logarytmów:

Zgadza się. Każdą liczbę naturalną można tak wyrazić: wystarczy wziąć stosowną liczbę pierwiastków kwadratowych.

I oto wniosek, który posłużył jako tytuł artykułu: w tym roku wszystko się uda, jeżeli tylko odpowiednio popracujemy.

***

Dla większych liczb do naszej zabawy wkroczą już bardziej zaawansowane funkcje matematyczne. Pierwsza jest prosta, to podwójna silnia, oznaczana podwójnym wykrzyknikiem: n!! Nie jest to „silnia silni”, tylko iloczyn kolejnych liczb, ale branych „co druga”, tak, że 2!!=2, ale 3!!=1·3=3, 4!!=2·4=8, 5!!=1·3·5=15, 6!!=2·4·6=48.

Poza tym mamy „silnię z przodu”, !n. Jest to liczba wszystkich permutacji n elementów, które nie mają punktu stałego. Z techniki „włączeń i wyłączeń” możemy wykazać, że jest ona równa

Wykorzystamy tylko początkowe wartości: !3=2, 4=9, !5=44. Taka silnia podaje odpowiedź do znanego zadania o „roztargnionej sekretarce”. Miała ona włożyć n listów do n kopert, ale wkładała je losowo. Jakie jest prawdopodobieństwo, że żaden nie trafił do właściwej koperty?

Sprawdźmy. Jeżeli są dwa listy, to prawdopodobieństwo jest oczywiście równe

Dla trzech listów: jeżeli adresatami są A, B, C, a mają do nich trafić w kolejności listy 1, 2, 3, to trzy pomyłki są możliwe tylko dla 231 i 312. Przy każdym innym rozkładzie przynajmniej jeden list trafi do właściwej koperty. Jeżeli adresatów jest czterech, „totalny bałagan” mamy w 9 przypadkach: 2341, 2341, 2413, 3142, 3412, 3421, 4123, 4312, 4321. 

Prawdopodobieństwem tego zdarzenia jest zatem 

Dla pięciu adresatów mielibyśmy 

Wspominam o tym dlatego, że ciekawym i nieoczekiwanym faktem jest, że prawdopodobieństwo to zbliża się to odwrotności liczby e. Mamy bowiem

Od zabawy liczbowej doszliśmy do rachunku prawdopodobieństwa i matematyki z poziomu maturalnego.

Możemy teraz rozszerzyć naszą tabelkę, na przykład

Aby dać sobie radę z liczbą 39, wspomnę zapis, który wymyślił Hugo Steinhaus (matematyk lwowski, a potem wrocławski, 1887–1972) do zapisywania bardzo wielkich liczb.

Otóż n w trójkącie oznacza u Steinhausa n podniesione do potęgi n. Liczba sama podnosi się do potęgi. Dziś moglibyśmy powiedzieć, że robi sobie selfie.

Na przykład: 

Dalej, mamy 3³=27, 4⁴=256, 5⁵=3125 i funkcja ta rośnie bardzo szybko.

Następnie, n w kwadracie znaczy: n w n trójkątach, czyli na przykład

Ale trzy w kwadracie to już:

czyli 27²⁷ podniesione do potęgi 27²⁷. To jest równe 1083-cyfrowej liczbie

Dalej, „n w kółku” to „n w n kwadratach”, na przykład

Wygląda to bardzo prosto, nietrudno stwierdzić, że jest to 256 w 256 trójkątach. Ale tego nie sposób obliczyć. Nie można nawet powiedzieć, ile ta liczba ma cyfr, a nawet ile cyfr ma liczba jej cyfr. Zacznijmy - wiedząc, że i tak się nie uda. 256 w trójkącie to 256²⁵⁶, a 256 w dwóch trójkątach to 256²⁵⁶ podniesione do potęgi 256²⁵⁶. Możemy pobawić się i obliczyć, że liczba cyfr liczby jej cyfr to 620 (to dobre ćwiczenie dla obcokrajowca z gramatyki polskiej). Na świecie jest około 7 miliardów ludzi, 7 000 000 000. Ta liczba ma dziesięć cyfr, a więc liczba cyfr liczby cyfr to 2…. Gdyby małe żyjątka o długości jednego milimetra ustawiły się w rządku przez cały widzialny Wszechświat, to liczbą cyfr liczby cyfr byłaby 27. A my mieliśmy 620. Próbując opanować liczbę „2 w kółku”, zrobiliśmy dwa pierwsze kroki z 256 do zrobienia i już „polegliśmy”. W dalszym ciągu będę pisać Δ2 zamiast „dwa w trójkącie” itp. Mamy:

Tabelkę można ciągnąć jeszcze bardzo długo i nie bardzo wiadomo po co. Dotykamy tu jednak problemu z pogranicza psychologii i filozofii. Wiemy, że liczb jest nieskończenie wiele. Jak je zapisać? Pierwszy zastanawiał się nad tym Archimedes. Trudno mu było pojąć nawet miriadę, czyli nasze dzisiejsze 10000. Po drugie: czy naprawdę liczb jest nieskończenie wiele, skoro i tak nie umiemy ich wszystkich ogarnąć. Tylko w teorii można dojść z Lizbony do Warszawy bez odpoczynku. Pierwszy krok postawimy, a jeżeli postawimy ileś, to na jeszcze jeden na pewno wystarczy nam siły. Takie paradoksy próbowało przezwyciężyć kilku matematyków.

***

Znaczenie informatyczne ma inny, podobny problem: wyrazić daną liczbę za pomocą… samych jedynek. Dopuszczalnymi działaniami są tylko dodawanie mnożenie, a chodzi o najkrótsze takie przedstawienie. Na przykład 2025 możemy złożyć,
dodając 2025 jedynek, ale wystarczą 22:

2025=(1+1+1)∙(1+1+1)∙(1+1+1)∙(1+1+1)∙((1+1)∙(1+1)∙(1+1)∙(1+1+1)+1)

Ale to temat na inny artykuł.

Z informatycznego punktu widzenia ważniejsze jest, ile operacji jest potrzebnych. Ile dodawań, ile mnożeń, chociaż dla współczesnych procesorów to niemal wszystko jedno. Ale to już łatwo obliczyć: jeżeli mamy n jedynek, to potrzeba n – 1
działań. Trudniej jest obliczyć – a to też ważne – ile par nawiasów jest potrzebnych. W podanym przykładzie aż 9.

Można wykazać (dowód nie jest łatwy), że do wyrażenia danej liczby za pomocą jedynek potrzeba ich około ln n³, gdzie log oznacza logarytm naturalny (przy podstawie e). „Około” znaczy tu, że im większa liczba, tym na ogół przybliżenie jest lepsze. Dla n=2025 mamy ln n³=22,8. Dla n=10000 przybliżenie logarytmiczne daje 28 i istotnie możemy mieć 28 jedynek:

10000=(1+1)∙(1+1)∙(1+1)∙(1+1)∙(1+1+1+1+1)∙(1+1+1+1+1)∙(1+1+1+1+1)∙(1+1+1+1+1)

Ogólniej, dla liczb 10ⁿ podobny sposób wymaga 7n jedynek.

Bywają lepsze: 3¹⁰ da się z 30 jedynek, a z oszacowania wychodzi 33.

Przyjrzyjmy się liczbie 111111111. Oszacujmy, ile potrzeba jedynek.

Oszacowanie logarytmiczne daje 55,56. Znaczy to tylko tyle, że możemy oczekiwać rozkładu z udziałem mniej więcej tylu jedynek. Zobaczmy, co się da zrobić. Tu już wchodzi matematyka z nieco wyższej półki. Wiąże to się z pewną „wyobraźnią liczbową”, także ważną w matematyce i jej zastosowaniach.

Rozłóżmy naszą liczbę w ten sposób. 111111111=9∙37∙333667=9∙37∙(2∙27∙37∙167+1) i zbierzmy informacje, ile jedynek potrzeba do wyrażenia składowych. Dziewiątkę uzyskamy z sześciu jedynek (jako trzy razy trzy). Do liczby 37 możemy dojść jedenastoma jedynkami (jako 37=4∙9+1=6²+1). Dwadzieścia siedem to potęga trójki (wymaga dziewięciu jedynek). Sto sześćdziesiąt siedem przedstawimy jako 3∙5∙11+2. Do liczb 3, 5, 11 i 2 potrzebujemy odpowiednio 3, 5, 8 i 2 jedynek. Teraz musimy zsumować:

6+11+2+9+11+3+5+8+2+1=58

Potrzebowalibyśmy 58 jedynek, a więc 57 działań, co jest mniej więcej zgodne z oszacowanie logarytmicznym. Być może dałoby się trochę mniej. Być może nie.

Michał Szurek