Myślenie ma kolosalną przyszłość
Psychologowie zastanawiają się, jak to jest z naszym myśleniem? Jak sądzisz, Czytelniku, jaką czynnością jest ono? Czy bardziej przypomina malowanie obrazu, czy jazdę na rowerze? Inaczej mówiąc, czy w wyniku myślenia powstaje coś naprawdę nowego, czy tylko zostają niewidoczne ślady, jak w leśnej ścieżce? Czy - jak widział to Sokrates - myślenie jest tylko przypominaniem sobie, wyciąganiem z głębi umysłu tego, co w nim siedziało zawsze - podobnie jak to było z wywoływaniem zdjęć w dawnych czasach (na naświetlonym papierze w ciemni wyłaniał się zwolna czarno-biały obraz), czy przeciwnie - nagle powstaje coś z niczego: "nie wiedziałem, a wiem"? Jak przechodzimy od początkowego "to dla mnie czarna magia", przez "nic nie rozumiem" i "zaczyna świtać", potem "oj, to chyba zrozumiem", do "zrozumiałem" i finalnego "ależ to było proste". Jak to się nam połączyło w jeden ciąg?
***
Nie wystarczy mówić do rzeczy. Trzeba mówić do ludzi.
Stanisław Jerzy Lec
Jeszcze trochę poteoretyzuję. Wspomnę o różnicy między rozumem a intelektem. Przekonuje mnie ujęcie Immanuela Kanta (1724–1804), filozofa z pruskiego Königsbergu, znanego pod polską nazwą Królewiec, a dziś, hm, wszyscy wiemy, jak się nazywa to miasto… Mówi anegdota, że Kant lubił rozmyślać, patrząc na daleką wieżę ratuszową. Z latami widok ten coraz bardziej przesłaniała mu topola (jak wiadomo, topole szybko rosną). Filozof rozkazał zatem ściąć drzewo. Wieża dotrwała do roku 1945, celny strzał radzieckiego artylerzysty zamienił ją w kupę gruzów.
Zauważyłem, że w swoich tekstach coraz bardziej gawędzę. No cóż, może to i przywilej wieku. Ale wracam do filozofii Kanta. Mówi on: rozum to zdolność myślenia. Intelekt to zdolność poznania. Intelekt ujmuje, opracowuje, przetwarza, systematyzuje i klasyfikuje to, co jest w zmysłach. Rozum stara się zrozumieć sens. W poznaniu dążymy do prawdy, w myśleniu do zrozumienia znaczenia.
Od czasów Oświecenia wierzymy w postęp określany jako właśnie jako nieograniczone poznanie, jako bezustanne dążenie do prawdy. Obecnie jesteśmy sceptyczni i sądzimy, że tak zwanej prawdy ostatecznej nie ma. W tym sensie Hannah Arendt (1906–1975) deprecjonuje rozum, pisząc, że pytanie znaczenie jest "pozbawione znaczenia" dla zdrowego rozsądku i rozumowania zdroworozsądkowego, ponieważ to do szóstego zmysłu należy dostosowanie nas do świata zjawisk i wprowadzenie nas do świata danego przez naszych pięć zmysłów; jesteśmy w tym świecie i żadne pytania nie muszą być stawiane. Może to i racja: jeżeli już zrozumiemy, dlaczego pies szczeka a kot miauczy, to… co z tą wiedzą zrobimy?
Wystarczy tej filozofii… Zgódźmy się, że rozum i intelekt mają się dopełniać - jak dzień i noc, lewo i prawo, parzyste i nieparzyste, orzeł i reszka, yin i yang, mężczyzna i kobieta.
Trójkąt. Foremki do ciasteczek mojej babci
Znam przerażenie młodych nauczycielek klas 1–5, które "muszą" uczyć i matematyki. Owszem, odpytują z tabliczki mnożenia i uciekają od nielubianego przedmiotu jak tylko mogą. Być może w ich rodzinach nielubianego od dwóch pokoleń. Pani profesor Anna Widur z UJ (która zanim została profesorką, uczyła przez kilkanaście lat w szkole podstawowej), napisała kiedyś ciekawy artykuł, którego tytuł mówi sam za siebie:
Jak ja mam lubić matematykę, skoro mój psor jej nie lubi?
Nic nie zastąpi bezpośredniego przeżycia. Wspominam piękną lekcję geometrii, jaką poprowadziła moja nauczycielka, Helena Sygnatowicz, gdy byłem w czwartej (!) klasie szkoły podstawowej. Na placu Lelewela (wtedy całkiem dzikim) na warszawskim Żoliborzu wytyczaliśmy w terenie linie proste, trójkąty i kwadraty. Jeszcze pamiętam, jak leżałem na zimnej trawie i krzyczałem do kolegów: "tyczkę bardziej w prawo".
Profesor Anna Krygowska (1904=1988), uznawana za guru w dziedzinie nauczania matematyki pisała, że nie należy "zmiękczać" matematyki, luzować ścisłości i w ogóle nie przesadzać z poglądowością. No cóż, przesadzać nie należy w niczym, ale w sprawie "zmiękczania" nauczania matematyki mam przeciwne zdanie. Dalszy ciąg artykułu można potraktować jako pewną propozycję stylu nauczania. Nie będę wkładał kija w mrowisko i nie wyślę go do fachowych periodyków dydaktycznych. "Młody Technik" i tak jest lepszy.
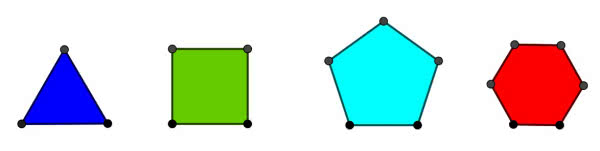
Mamy 2022. Znajdź, mój wnuku, trzy patyczki i spróbuj ułożyć z nich trójkąt. Czy zawsze się to uda? Nie zawsze - jeżeli jeden będzie bardzo długi, a dwa inne krótsze, to nie uda im się objąć długiego, prawda?
Ale jeżeli patyczki będą równe, to trójkąt da się zbudować - i to całkiem równy. To znaczy taki sam w każdą stronę. Nazywamy go foremnym. Wiesz, kiedy pierwszy raz usłyszałem tę nazwę, to pomyślałem sobie, że to pochodzi od foremki na ciasteczka. Pamiętam, że moja babcia Franciszka miała takie foremki; zresztą różnych kształtów. Ciasteczka babci miały niepowtarzalny smak, ale mnie fascynował ich kształt (3).
Równe boki, równe kąty. Wielokąty foremne
Staś i Ala robią sałatkę na kolację.
- Dzieci! Moje kochane bliźniaki! Robicie kolację!
Mama i tata są zmęczeni po pracy i pójdą na spacer do parku.
- Ale my się uczymy geometrii. Była lekcja o trójkątach i figurach foremnych i mamy pracę domową: znaleźć pomysłowe trójkąty, sfotografować i wysłać pani.
- Zdążycie po kolacji. My dawno nie byliśmy tylko we dwoje, a wy macie już 11 lat. Dacie radę.
Staś chciał dalej protestować, ale Ala wpadła na pomysł.
- Możemy połączyć jedno z drugim. Słyszałam, jak pewien starszy profesor mówił, że matematyka jest wszędzie. Zrobimy sałatkę. Wyjmij trzy jajka z lodówki. Tylko ostrożnie. Nie stłucz. W porządku. Ustaw je ładnie w trójkąt.
- Ale jak?
- Nie zadawaj głupich pytań. Ustaw.
- Może być tak?
- Bardzo dobrze. Daj komórkę, zrobię zdjęcie.
Dorysujemy potem trzy kreski i będziemy mieli trójkąt. Trójkąt jajeczny. Teraz weźmiemy pomidory. Połóż na stole.
- Już położyłem. Wystarczy sześć?
- Braciszku, trochę za dużo. Ale jak ładnie leżą.
Mamy trójkąt pomidorowy.
– Czyli tomato triangle.
– Yes. Popatrz, w kolejnych warstwach mamy: jeden pomidor, dwa, trzy. Czy w następnej będą cztery?
- Nie wiem, nie mamy już pomidorów.
- Weź rzodkiewki. Popatrz. Najpierw jest jedna rzodkiewka, potem dwie, trzy, cztery i pięć. Razem 1+2+3+4+5 = 15.
Rzodkiewki są sprzedawane w pęczkach po 10 sztuk. Dwa pęczki
nie wystarczyłyby. W liceum poznasz sposób obliczenia,
ile rzodkiewek jest w takiej piramidce o wielu rzędach
- To potem będzie 1+ 2+ 3 + 4 + 5 + 6 = 21, potem jeszcze siedem, czyli dwadzieścia osiem, a potem trzydzieści sześć, czyli sześć razy sześć. Czy mamy 36 rzodkiewek? Ułożymy je w kwadrat 6 na 6.
- Stasiu, po pierwsze nie mamy tyle, po drugie 36 rzodkiewek w sałatce to starczyłoby dla całej klasy. A jeszcze przecież rzodkiewki są ostre. I tak wyjdzie nam dziwna sałatka.
- Może jeszcze dokroimy ogórek? W przekroju otrzymamy ładne elipsy?
- Mama mówi, że ogórek kłóci się z pomidorem w jednej misce. Zostawmy, jak jest.
- Może i dziwna, ale piątkę z pracy domowej mamy na pewno. A widelce dla Rodziców i dla nas ustawimy w czworokąt foremny.
- Czyli w kwadrat? Cztery równe boki i cztery kąty proste?
- No, tak.
- Mam pomysł. Postawimy miskę sałatki na sześciu podstawkach ustawionych w sześciokąt. Przynieś i ustaw. O tak, bardzo dobrze. Kolacja prawie gotowa. Tylko jeszcze trzeba ugotować jajka, pokroić pomidory i rzodkiewki. Dodamy szczypiorku i twarożku, trochę jogurtu. Daj komórkę, sfotografujemy.
(…)
- Dzieci! Zrobiłyście kolację? Pomożemy wam potem w matematyce.
- Nie trzeba, mamusiu. Już wszystko gotowe. Kolacja i praca domowa z geometrii.
- Naprawdę? Och, jaka pyszna i estetycznie podana sałatka.
- Tak? Ten starszy pan, który mówił, że matematyka jest wszędzie, powiedział też, że "matematyk zrobi to lepiej". Czy to prawda, tatusiu?
ułożonych w sześciokąt. Powtórzą jeszcze biologię:
jakie ptaki są na podstawkach. U góry i po prawej
to oczywiście dzięcioły. Potem kolejno zięba,
zimorodek, szczygieł i kowalik
Matematyka jest kolorowa
W 1974 roku zaczęła się ukazywać Delta - miesięcznik popularnonaukowy Polskiego Towarzystwa Matematycznego i Polskiego Towarzystwa Fizycznego. W 1983 roku dołączyło PTA ("A" jak Astronomia). Po kilku miesiącach stosowne gremia zebrały się, by ocenić unikatowe przedsięwzięcie - popularne czasopismo, redagowane przez czynnych pracowników naukowych. Skądinąd bardzo zasłużony profesor XY mocno skrytykował graficzną stronę numerów. "Matematyka nie potrzebuje kolorów" stwierdził. "Jest poważną nauką i nie przystoi jej pstrokacizna".
Od tego czasu zmieniło się bardzo wiele - bez kolorowych rysunków nie wyobrażamy sobie podręcznika. Więcej - zagadnienia "kolorowania grafów" okazały się ważnymi zagadnieniami matematycznymi, z zastosowaniami do teorii przepływów w sieciach.
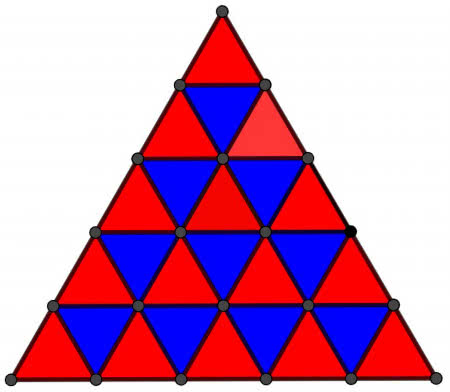
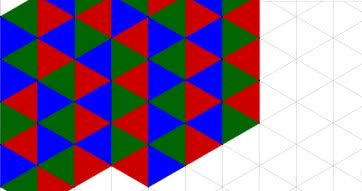
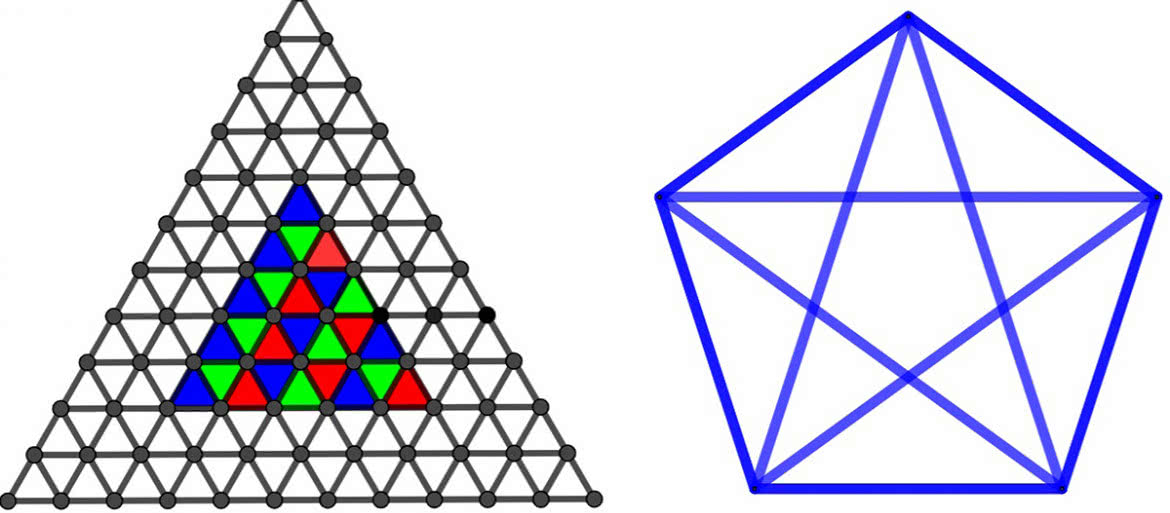
W szkole na trójkąt foremny mówi się równoboczny. Z takich trójkątów możemy ułożyć siatkę i nawet ją pokolorować, jak szachownicę. Na rysunku 10 mamy siatkę dwukolorową. W każdym oczku spotykają się dwa kolory. Są trzy trójkąty niebieskie i trzy czerwone. Każdy czerwony jest otoczony przez trzy niebieskie, a każdy niebieski przez trzy czerwone. To znaczy, że po jednej stronie każdego odcinka jest czerwono, a po drugiej niebiesko. Na rysunkach 11 i 12 użyłem trzech kolorów. Przestrzegałem zasady, żeby w każdym punkcie (węźle siatki) spotykały się dwa czerwone, dwa niebieski i dwa zielone - a także, by trójkąty tego samego koloru nie miały wspólnego boku. Stwórz własne kolorowanki.
Stanisław i Alicja na uniwersytecie
Po latach…W swojej pracy licencjackiej na wydziale matematyczno-informatycznym dobrego uniwersytetu Stanisław napisał pracę licencjacką, analizując podobne zadanie na bryłach foremnych dowolnego wymiaru. Na stosownym seminarium dowiedział się o bryłach dualnych. Przez połączenie środków ścian sześcianu powstaje bryła do niej dualna - ośmiościan foremny. Dwunastościan jest dualny do dwudziestościanu, a czworościan jest autodualny - jest dualny sam do siebie.
Alicja zajęła się zastosowaniami, algorytmiką, optymalizacją i przepływami w sieciach - przydał się jej rysunek 12. Jak najlepiej przesłać informacje z punktu A do punktu B po danej sieci wielokątnej? Jak chronić się przed cyberatakami?
Rodzeństwo odwiedza często swoich rodziców. Na kolację jest zwykle sałatka z jajek, pomidorów, rzodkiewek i ogórków z dodatkiem szczypiorku i twarożku. Widelce ustawiają jeszcze w kwadrat. Ich rodzice nie mają jeszcze wnuków. Ale czekają.
Zakończenie. Każdy nauczyciel matematyki spotkał się wiele razy z pytaniem uczniów (a także ich rodziców): po co mi (mojemu synowi, mojej córce) to wszystko? Co mu/jej w życiu przyjdzie z tego, że będzie znał/a wzór na sinus kwadrat plus cosinus kwadrat? Nauczyciele próbują podawać liczne zastosowania matematyki, ale nie tędy droga. Należy rozszerzyć pytanie: co mu/jej przyjdzie ze znajomości przebiegu wojen napoleońskich, układu rozrodczego pszczoły, znajomości Pana Tadeusza i życiorysu Stanisława Wokulskiego, życiu wymarłych gadów, symfonii Beethovena, geografii Ameryki Północnej, wzoru na drogę w ruchu jednostajnie przyspieszonym… i tak dalej i tak dalej.
Wniosek jest jednoznaczny. W szkole mogłyby być tylko dwa przedmioty: język angielski i obsługa Windows.
Michał Szurek