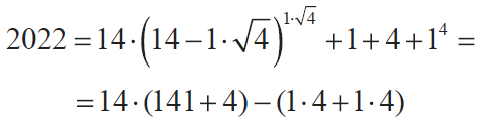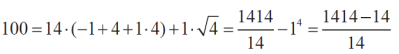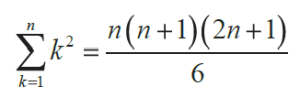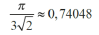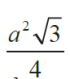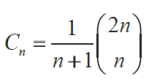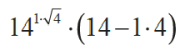Gawęda wakacyjna o czternastce

Ale to nie matematyka… Pierwsze ćwiczenie: czy da się wyrazić 2022 za pomocą samych cyfr 1, 4, użytych właśnie w tej kolejności? Zadanie nie do końca sprecyzowane; oto zatem rozwiązanie, z którego każdy domyśli się reguł gry.
Zauważmy, że w pierwszej równości "czternastkę" wykorzystujemy sześć razy - dokładniej: sześć razy następstwo cyfr 1 i 4. W drugiej równości tylko pięć razy. Można oczywiście spróbować z innymi liczbami. Na przykład:
Tutaj "czternastkę" wykorzystujemy po cztery razy. Powtórzę, że nie chodzi o samą liczbę, tylko o następstwo cyfr 1 i 4.
Zabawę można przedłużyć na przykład na ważne daty z historii Polski. Zacznijmy od bitwy pod Grunwaldem.
A oto koniec PRL:
Zatrzymajmy się przy tych dwóch przedstawieniach daty przełomu w polskiej historii współczesnej. Który z nich jest "lepszy"? To oczywiście zależy od kryteriów, ale można powiedzieć, że pierwszy potrzebuje tylko pięciu "czternastek", a drugi sześciu. Poza tym pierwszy jest bardziej pomysłowy, bo używa silni. Przypominam, że silnia (oznaczana wykrzyknikiem po liczbie) to iloczyn kolejnych liczb - tak jak tutaj:
1!=1, 2!=1·2=2, 3!=1·2·3=6, 4!=1·2·3·4=24, 5!=1·2·3·4·5=120, ...
Wartości funkcji silnia rosną bardzo szybko, o czym można się przekonać, włączając kalkulator.
W zadaniu chodzi zatem również i o to, by otrzymać daną liczbę możliwie zgrabnie, bo przecież można dodawać same 14 i też dostaniemy, co trzeba.
Czy jednak takie zadania mają sens? Rozrywkowy na pewno tak, ale nawet i nieco kształcący. Proste obliczenia powinniśmy umieć wykonywać szybko, bez oglądania się na elektronikę. Nawet gdy są koparki, trzeba umieć wykopać dołek łopatą.
Większe znaczenie ma takie oto zadanie: wyrazić liczbę, powiedzmy właśnie 14, za pomocą jak najmniejszej liczby dodawań i mnożeń samych jedynek. Nie można tych cyfr łączyć do 11, 111 i tak dalej. Można dodawać same jedynki, ale to nieekonomicznie. Zróbmy tak:
14=(1+1)·((1+1+1)·(1+1)+1)
Mamy zatem liczbę 14 wyrażoną za pomocą ośmiu jedynek, stosunek 14:8. To mało oszczędnie. Dla większej liczby 27 wystarczy dziewięć jedynek:
27=(1+1+1)(1+1+1)(1+1+1)
Niektóre liczby są bardzo mało wymagające, oczywiście w stosunku do swoich wielkości. To przede wszystkim potęgi dwójki, np.:
64=(1+1+1+1)(1+1+1+1)
osiem jedynek, stosunek 64/8=8.
1024=(1+1+1+1)(1+1+1+1)(1+1+1+1)(1+1+1+1)(1+1+1+1)
- dwadzieścia jedynek, 1024/20=51,2.
2048=(1+1+1+1)(1+1+1+1)(1+1+1+1)(1+1+1+1)(1+1+1+1)(1+1+1+1)
- dwadzieścia cztery jedynki, stosunek 2048/24>85. Jednak niewiele większa 2187 ma znacznie lepszy wynik:
2187=(1+1+1)(1+1+1)(1+1+1)(1+1+1)(1+1+1)(1+1+1)(1+1+1)
- dwadzieścia jeden jedynek, stosunek 2187/21 to już ponad 100.
Można zrozumieć, że potęgi trójki są tu lepsze niż potęgi dwójki. To ma pewne znaczenie informatyczne.
Ale miało być o liczbie 14. Porzućmy dziwną arytmetykę i zajrzyjmy do literatury. Pan Tadeusz, czyli ostatni zajazd na Litwie. Telimena mówi do Zosi:
Wszak to dziś zaczynasz
Rok czternasty, czas rzucić indyki i kurki.
A jak się nazywał kochanek dziewczyny, o której tu mowa niżej (wskazówka: nazwisko Montecchi).
PANI KAPULET
Marto, pozostań; przychodzi mi na myśl,
Że twa obecność może być potrzebna.
Julka ma piękny już wiek, wszakże prawda?
Czternaście ma już lat, jak mi się zdaje.
(przekład Józefa Paszkowskiego)
A oto inne pytanie z literatury. Co jest ciekawego w Psalmie XI Jana Kochanowskiego? Odpowiem: jest napisany 14-zgłoskowcem symetrycznym (to znaczy 7+7, siedem sylab i siedem). To bardzo nietypowe metrum (pisownia oryginalna):
Panu ja ufam, a wy mówicie: między góry.
Uciekaj co nadalej jako ptak prędkopióry;
Twój nieprzyjaciel łuk wziął, strzałę ma na cięciwie
Myśląc, jakoby z cienia dobre strzelał zdradliwie.
Natomiast jako przykład asymetrycznego czternastozgłoskowca (6+8) przypomnijmy sobie Trzech Budrysów:
Stary Budrys trzech synów, tęgich jak sam Litwinów…
Wróćmy do matematyki. Nasza liczba jest sumą kwadratów trzech początkowych liczb naturalnych: 12+22+32=14. Znany nauczycielom ogólny wzór na sumę kwadratów to:
Można to zobaczyć, układając piramidkę z kulek (1) albo sześcianów (2), 1+4+9=14.
Liczba 14 ma związek z lądowaniem na Marsie. Spójrzmy na bryłę widoczną w dwóch ujęciach. Na fotografii 3 mamy na nią widok "z góry" - widać siedem kulek, inne siedem jest pod spodem, ale pod środkową znajduje się jeszcze jedna - jej fragment widać na fotografii 4. Jest ona zatem opatulona przez czternaście przylegających do niej. I o to chodziło. Zewnętrzne kulki były balonikami, a właściwa sonda znajdowała się wewnątrz środkowej kuli. Chodziło o to, żeby całość nie potoczyła się za daleko (tak by było, jeżeli to by była jedna kula), ale i nie zakantowała gwałtownie (gdyby to było pudełko sześcienne). Właśnie taka bryła zapewniała rozwiązanie pośrednie. Jak to się często zdarza, trzeba było tylko sięgnąć do skarbnicy wiedzy matematycznej.
Na fotografii 5 widzimy inną, niepozorną bryłę, sklejoną z czternastu kulek. Takie bryły pasują jedna do drugiej, 3 można nimi wypełniać przestrzeń. Oczywiście nie całą przestrzeń - kule nie mogą jej wypełniać bez wolnych pól. Tylko sześciany się do tego nadają. Ale takie właśnie ułożenie jest najgęstszym możliwym układem - a właściwie jednym z dwóch najgęstszych. Drugim jest ustawienie kulek w czworościenną piramidkę - taką, jaką ułoży każda przekupka, sprzedająca pomarańcze na targu. Obydwa ustawienia zapełniają tyle samo miejsca w przestrzeni - niecałe 75%, dokładna wartość to:
Odkrycie to ma ciekawą historię. W 1611 oku Johannes Kepler wyraził przypuszczenie, że tak właśnie jest - kul nie da się upakować gęściej. Pełny dowód, że przypuszczenie jest prawdziwe, jest dziełem amerykańskiego matematyka Thomasa Halesa i został ogłoszony w… 1998 roku, a więc stosunkowo szybko, bo zaledwie w 387 lat po Keplerze. Hales wykorzystał zresztą stary pomysł László Fejesa Tótha z 1953 roku. Ale recenzenci, którzy przeczytali pracę, orzekli, że dowód jest poprawny tylko na 99%; no a skoro mamy do czynienia z matematyką, to ma być 100%. Hales wziął się do pracy i już po 16 latach (czyli w 2014 roku, dokładnie 10 sierpnia) podał nowy dowód, oparty zresztą na technice automatycznego dowodzenia twierdzeń i tym razem wszystko już zagrało. Dowód został zaakceptowany, a sprzedawcy w sklepie warzywnoowocowym dostali uzasadnienie, że układają swoje piramidki w majestacie matematyki. Sądzę, że odetchnęli z ulgą, ale nie pytałem pani Eli, sympatycznej właścicielki sklepiku, w którym kupuję.
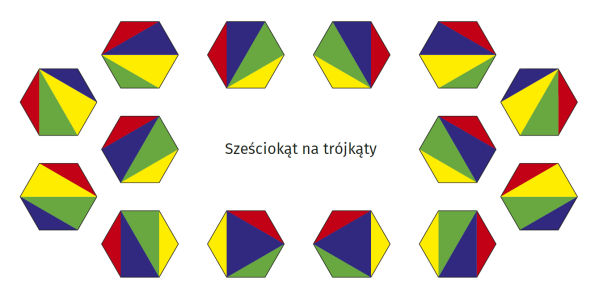
Na wielu zajęciach polecam uczniom - a także nauczycielom - ułożyć z klocków bryły o 14 ścianach. Niektóre takie bryły widzimy na fotografii 6. Jest dużo innych, ciekawych. Jakoś tak jest, że właśnie czternaście ścian daje interesujące układy.
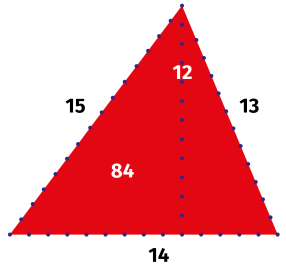
Spójrzmy teraz na "prawie równoboczny" trójkąt - o bokach długości 13, 14, 15, a zatem o obwodzie 42. Jest on interesujący dlatego, że i pole wyraża się liczbą całkowitą. To nie takie częste wśród trójkątów nieprostokątnych. Spójrzmy.
Pole trójkąta równobocznego o boku a to
a zatem jeżeli a jest liczbą całkowitą, to pole jest liczbą niewymierną. Inne trójkąty "prawie równoboczne" o podobnej własności też mają coś wspólnego z liczbą 14, na przykład następnym takim trójkątem jest o bokach długości.
193, 194=142–2, 195,
a cała seria wygląda tak:
13, 14, 15
(142–2)–3, 142–2, (142–2)–1
(142–2)2–3, (142–2)2–2, (142–2)2–1
i tak dalej. Jest to po prostu rekursja czy, jak kto woli, indukcja:
b1=14, bn+1=bn2–2
Liczba 14 jest też jedną z liczb Catalana Cn (belgijski matematyk, Eugène Charle Catalan 1 14–1894). To ciekawe liczby, pojawiające się tu i tam w całej matematyce. Przytoczę najpierw sztywne określenie, które powinno być zrozumiałe dla licealistów:
A zatem
Zobaczmy. Oto pierwszy przykład: na ile sposobów można podzielić wielokąt o n bokach na (n–2) trójkątów? Łatwo się przekonać, że kwadrat można podzielić na dwa sposoby (tniemy wzdłuż jednej albo drugiej przekątnej), pięciokąt na pięć, a sześciokąt właśnie na czternaście (8).
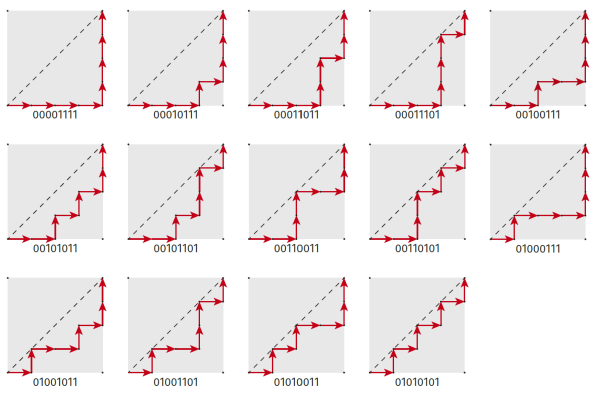
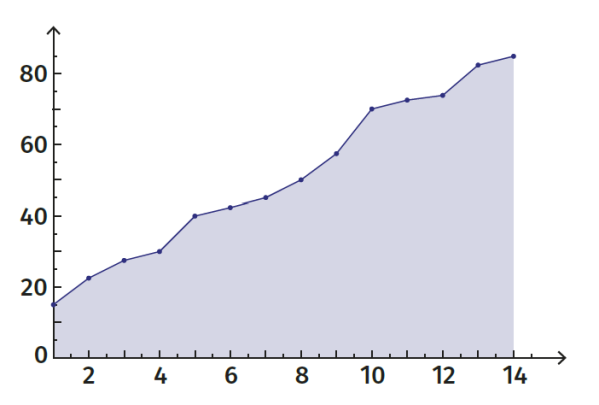
Większe znaczenie mają liczby Catalana w analizie przepływów w sieciach. Z kilku interpretacji wybiorę rekreacyjną, "spacerową". W uroczym uzdrowisku chodzę codziennie po alejkach parkowych, od południowo-zachodniego narożnika do północno-wschodniego. Jednak połowa parku jest zamknięta i nie mogę przekraczać narysowanej przekątnej. Czy wystarczy mi tras na dwutygodniowy pobyt, jeśli chciałbym każdego dnia maszerować choć trochę inaczej? Tu właśnie pomaga mi Eugène Calatan. Jest akurat czternaście możliwych tras (9). Mogę je zakodować za pomocą zer i jedynek: zero to na wschód, jedynka - do góry. Mogę przerobić kody binarne na liczby dziesiątkowe i przypomnę sobie Babią Górę. Dlaczego? Spójrzmy na rysunek 10. Czy to nie jest podejście na Babią od wschodu? Przypomnę, że wysokość Babiej Góry (najwyższego poza tatrzańskiego szczytu w Polsce) to:
metrów nad poziom morza.
Jakie to liczby? Przetłumaczmy z dwójkowych na dziesiętne.
1111 dwójkowe to: 8+4+2+1=15,
101112 to 16+4+2+1=23,
110112=16+8+2+1=27,
111012=16+8+4+1=29,
1001112=32+4+2+1=39,
1010112=32+8+2+1=43,
1011012=32+8+4+1=45,
1100112=32+16+2+1=51,
1101012=32+16+8+1=57,
10001112=64+4+2+1=71,
10010112=64+8+2+1=75,
10011012=64+8+4+1=77,
10100112=64+16+2+1=83
i wreszcie ostatnia: 10101012=64+16+4+1=85
Czy nie znudziłem Cię, drogi Czytelniku, tymi liczbami? Może i tak. Jest lato, może jesteś w górach…, ale spójrz jeszcze na ciąg, ten od 15 do 85. Widzisz, że wszystkie liczby są nieparzyste. Czy widzisz powód, dla którego tak jest? Na pewno! No bo w jakim kierunku prowadzi ostatnia strzałka na rysunku 9?
Zaprawdę, 14 to ładna liczba. Kiedyś miałem 14 lat. Kiedy? Cóż, trochę dawno, był to rok
Michał Szurek