Same dwójki
Z mojego poletka rok 2022 będzie się też wstydzić, że widział pociągnięcia, świadomie cofające szkołę do tuwimowskiego Ciemnogrodu.
Dałoby się znaleźć więcej symboli związanych z dwójką, ale nie przesadzajmy. Zanim przejdę do takiej "matematycznej matematyki", rozejrzę się dokoła, poszukam tu i ówdzie liczby 2. Przenika całe nasze życie.
Mamy naturalną skłonność do patrzenia na świat w kategoriach kojarzenia par, analizy przeciwieństw, dążenia do symetrii, znajdowania uzupełnień i szukania odwrotności. Co mają ze sobą wspólnego słowa: symetria, odwrotność, znak, przeciwieństwo, pojedynek, mecz, ślub, lustro, symetria, duet, tandem, bliźniak, para, dopełnienie, podwoić? Właśnie liczbę dwa. Doceniam taniec solo, ale jakoś kojarzy mi się to z wirującą parą K+M.
I tych dwoje nad dwiema,
Co też są, lecz ich nie ma…
(Julian Tuwim, Kwiaty Polskie)
Gdziekolwiek jest przód, jest i tył, gdzie jest lewo, jest i prawo, góra idzie w parze z dołem, prawda z fałszem. Moneta ma awers i rewers (u nas mówimy na to orzeł i reszka, jak to będzie po przyjęciu euro?). Mąż jest mężem dlatego, że ma żonę i odwrotnie: kobieta zamężna jest w parze z jakimś mężczyzną. Czymże byłby Raj bez perspektywy Piekła? Gdyby nie było plusa, to i minus byłby niepotrzebny. Nie ma tego złego, co by na dobre nie wyszło.
W mitologii greckiej występowała para nierozłącznych przyjaciół: Orestes i Pylades, w rzymskiej: Kastor i Polluks; wspomnijmy też Sherlocka Holmesa i dr. Watsona, Flipa i Flapa (Stan Laurel i Ollie Hardy, komicy amerykańskiego filmu z lat 1919-1951), a starsi Czytelnicy kojarzą na pewno Jerzego Wasowskiego i Jeremiego Przyborę. Każdy, kto uczył się języka obcego, zaliczył odpowiednie ćwiczenie: określ antonim danego słowa: pełny-pusty, gruby-chudy, szeroki-wąski. To znany z logiki podział dychotomiczny, najprostsza klasyfikacja pojęć i rzeczy: na dwie klasy. Tak-nie. Lewo-prawo. Czarne-białe.
Teraz zadanie, które spora część Czytelników być może skomentuje: „w porządku, ładne, ale nie pasuje do kącika matematycznego!”. A ja sądzę, że bardziej pa-suje do matematycznego niż do jakiegokolwiek innego.
Zadanie 1
Co to znaczy "po dwakroć" i "w dwójnasób"? Co to znaczy, że rycerz pojechał "samowtór" zabić smoka? Czy "wtórnik" to to samo, co "duplikat"? Co to znaczy "wtórować", a czym jest "bisować"? Czy wiesz, że w dawnych czasach, gdy chłop pracował w polu, przynoszono mu obiad w dwojakach? Czy to to samo, co "podwoje". Czy "podwoić" to to samo, co "powtórzyć"? Gdzie jest w Tatrach Dwoisty Stawek (zwany inaczej Dwoiśniakiem)?
Czy zgodzisz się z tym, że każdy kij ma dwa końce? Co znaczy powiedzenie, że pokorne cielę dwie matki ssie? Nie znasz pewnie łaciny i nie rozumiesz, co znaczy bis dat, qui cito dat? Aha, i mam nadzieję, że "mieć dwie lewe ręce" nie odnosi się do ciebie. No i że nie jesteś dwulicowy (ani dwulicowa!).
Co to za zwierzę "cwajnos". Czy może widziałeś, ale nie w zoo, wielbłąda dwugarbnego? Czy wiesz, że na jeziorach mazurskich bardzo lubię obserwować perkozy dwuczube? Iluosobową grą jest brydż? Ile luf ma dubeltówka? Co to znaczy "kręcić dubla", "dać dubla", dubler, dublować? Jak się nazywa gra podwójna w tenisie? "Dwójniak" - jaki to miód? Co to jest dwutakt? Czy wiesz, że za moich szkolnych czasów ocena 2 znaczyła "niedostateczny" (tak jest i teraz w uczelniach wyższych).
No, dobrze, teraz będzie łatwo, to znaczy będą zadania matematyczne.
Zadanie 2
Ile osi symetrii mają następujące figury: prostokąt (niebędący kwadratem), romb (też niekwadratowy) elipsa (niebędąca okręgiem). Czy znasz figurę, która ma dwie (i tylko dwie) osie symetrii, ale nie są one prostopadłe?
Zadanie 3
Trójkąt ma trzy kąty, czworokąt cztery, a siedemnastokąt siedemnaście. Logiczne, prawda? Jaką figurę nazwałbyś dwukątem? Takich figur nie rozważa się w matematyce, ale co ci szkodzi pofantazjować?
Zadanie 4
Wiesz oczywiście, to jest "silnia" liczby n. Przypomnę: to iloczyn kolejnych liczb od 1 do n. Silnię oznaczamy przez postawienie wykrzyknika, a zatem 1!=1, 2!=2, 3!=6, 4!=24. Kalkulator poda nam jeszcze dokładną wartość 22!=1 124 000 727 777 607 680 000 - całkiem ciekawe ułożenie cyfr. Ale oto zadanie: uporządkuj liczby według wielkości: 2022!, 20!·22!, 20222022, 20!22!. To nie jest zadanie rachunkowe, tylko logiczne!
***
Nasza intuicja i zdrowy rozsądek płatają nam niekiedy figle. Już Sokrates zdołał wytłumaczyć pewnemu chłopcu - rysując figury na piasku, że podwojenie kwadratu to nie to samo, co podwojenie boku. Oto typowy rysunek (1). Mówiąc ogólnie, podwojenie wymiarów liniowych figury zwiększa pole czterokrotnie.
Wielu studentów geografii (a uczyłem na tym wydziale uniwersytetu) nie mogło intelektualnie pojąć czegoś takiego: Polska ma ok. 650 km "wszerz" (Słubice - Terespol 660) i 750 "z góry na dół" (Rozewie - Zakopane). Na mapie w skali 1 do miliona to jest 66 cm na 75 cm. Skoro jest nas w kraju około 38 milionów, to na takiej mapie powinno się zmieścić 38 ludzi! A jakoś byłoby trudno!
No, ale Czytelnikom "Młodego Technika" nie trzeba przecież wyjaśniać, gdzie w rozumowaniu jest błąd!
Zadanie 5
Jak podwoić trójkąt równoboczny? Chodzi o rozwiązanie geometryczne.
Rozwiążę tutaj. Jeżeli trójkąt ma bok długości a, to trójkąt o podwojonym polu będzie miał bok a√2. Wystarczy narysować kwadrat o boku a i na jego przekątnej zbudować trójkąt równoboczny. Ale z dwóch trójkątów da się złożyć jeden efektywniej i efektowniej (2). Może narysujesz, wytniesz i zobaczysz, że "się zgadza"?
Jak przebiega podział, który widzisz na rysunku 2? Wyjaśnia to następny rysunek 3.
Na boku danego trójkąta budujemy kwadrat i od jego boku CD odejmujemy połowę przekątnej. Zostaje odcinek EC. Budujemy trójkąt FCJ równoboczny takim boku: FC=CJ=FJ=EC=r. Odejmujemy połowę przekątnej. Na boku AC trójkąta odmierzamy odcinek r i budujemy trójkąt równoboczny FGH. Oznaczamy przez K punkt przecięcia prostej AH z bokiem BC. Pozostaje pokolorować wielokąty… Jeszcze tylko jedna uwaga. Wydaje się, że prosta AK jest prosto-padła do boku BC. Nie jest! Wykażę rachunkowo. Przyjmijmy, że boki trójkąta ABC mają długość 1.
Wtedy
zatem:
Na rysunku 3 widać, że bok JK pasuje do trójkąta równobocznego FCJ, a więc ma długość CJ=r, czyli 
Na odcinek KB zostaje więc 1-2r = √2-1. To w przybliżeniu jest 0,4142. Gdyby AK była prostopadła do BC, punkt K leżałby w połowie boku, czyli byłoby KB=0,5.
I jeszcze efektowny podział sześciokąta foremnego na dwa mniejsze, też foremne (4).
***
Czy można się rozdwoić na cztery części? Czy mogą być większe i mniejsze połowy?
Podam "rozwiązanie" od razu, dobry żart jest tynfa wart. W wierszu Poeta subtilis Leopolda Staffa (1878-1957), naszego wybitnego poety, debiutującego jeszcze w epoce Młodej Polski, czytamy: Rozdwoiłem się na cztery części.
Inny przykład: jeżeli mamy duże i małe jabłko, to ich połowy będą nierówne! W dodatku przecież z nierównymi połowami spotykają się codziennie rybacy i wędkarze: raz łowią więcej, a raz mniej!
Sześćdziesiąt lat temu chłonąłem książkę Karola Olgierda Borchardta (1905-1986) Znaczy Kapitan. Były to zbeletryzowane wspomnienia autora, późniejszego kapitana żeglugi wielkiej, z lat, kiedy powstała Polska z wąskim dostępem do Bałtyku. W pierwszych latach kadra dowódcza składała się z Polaków, którzy byli oficerami we flotach krajów zaborczych. Czasami coś im się mieszało. Autor cytuje jednego z oficerów z długoletnią służbą w marynarce rosyjskiej: Naszu otczizna rozćwiartowno na trzy nierówne połowy. Jednu połowu wziali Giermancy, drugą Awstrijcy, nu a trzecią my!
***
Wróćmy do trójkąta równobocznego. Jak go rozciąć na pół? Nietrudno - wystarczy ciąć przez wierzchołek i prostopadle do podstawy.
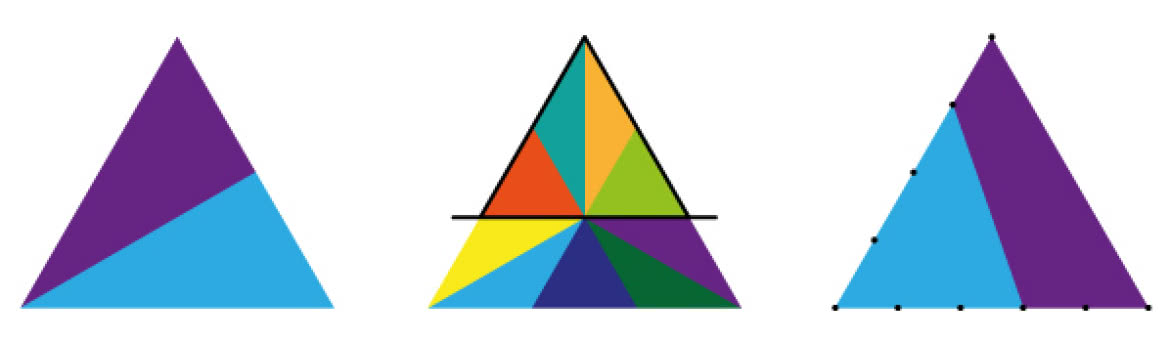
Czy każda prosta przechodząca przez środek trójkąta (mówimy o równobocznym) dzieli go na połowy? Oczywiście, że nie! Spójrzmy na środkowy trójkąt na rysunku 5. Każdy z kolorowych trójkącików ma to samo pole, górna część dużego trójkąta ma 4 części, a dolna 5. Stosunkiem pól nie jest 1:1 a 4:5.
Zadanie 6
Uzasadnij, że wszystkie "małe" trójkąciki środkowego trójkąta na rysunku 5 mają równe pola. A ile trójkątów widzisz na tym rysunku?
Zadanie 7
Wyznacz stosunek pól figur w trzecim trójkącie na rysunku 5.
Warto wiedzieć, kim był Henry Ernest Dudeney (1857-1931) - a nawet jego ojciec John, który pasał owce, jeszcze w XVIII wieku. To zajęcie daje trochę wolnego czasu i wtedy John Dudeney uczył się matematyki z książek, które kupował za swoje niewielkie wynagrodzenie. Nauka się opłaciła - został potem nawet kierownikiem szkoły w lokalnym miasteczku. Henry też zainteresował się matematyką - na poziomie ciekawych zadań i łamigłówek. Niektóre są interesujące. Oto jedna z nich.
Zadanie 8
Jak widzisz, mnożna i wynik mają po dziesięć cyfr. Czy mogą być one wszystkie różne (i nie uznajemy zera na początku liczby)? Aha, jeżeli nie pamiętasz, co to jest mnożna i mnożnik, to sobie przypomnij. Można zapamiętać, że mnożnik to jak robotnik. Robotnik robi, mnożnik mnoży (w tym przypadku przez 2). Podobnie dzielnik dzieli! Co dzieli? Oczywiście dzielną.
Zadanie 9
Matematyka to nie wszystko. Rodzeństwo, Ania i Bartek, odziedziczyło dość duży plac na przedmieściu, na skrzyżowaniu ulicy Głównej i Leśnej, między szosą i lasem, podzieloną notarialnie na 16 działek. Chcieli ją podzielić na równe części, bez naruszania granic tych działek. Po dyskusji podzielili plac tak, jak na rysunku 6. Oboje byli bardzo zadowoleni z takiego rozwiązania. Znajdź powody, dla których mogłoby tak być.
***
Komentarz do zadania 1
"Po dwakroć" to takie wzniosłe "dwa razy". W zaklęciach częściej pojawia się "po trzykroć". "W dwójnasób" to też "podwójnie", najczęściej w zbitce "w dwójnasób wynagrodzić" np. kogoś za wyrządzoną mu krzywdę. Rycerz wybrał się na walkę "samowtór" - to znaczy niby sam, ale z jednym giermkiem (gdyby giermków było więcej, to jechałby samotrzeć, samoczwart i samopiąt). Wtórnik to istotnie spolszczony duplikat, choć odnosi się raczej tylko do dokumentów (np. prawo jazdy).
Wtórować to znaczy mniej więcej "robić to samo, naśladować". Zapamiętałem rym: doktor na świni galopuje, a syneczek na zadzie mu wtóruje. Głupi, ale zabawny, a w książce, z której pochodził, miał określone znaczenie. Powtórzyć a podwoić to jednak co innego, prawda, chociaż niekiedy jest tym samym. Jeżeli wziąłem powtórnie porcję lodów, to tak, jakbym zjadł podwójne. "Podwoje" obecnie występują tylko w zwrotach "gościnne podwoje, otworzyć podwoje", a więc przyjąć, ugościć po przyjacielsku. Jeżeli ładnie coś zagrasz, to może poproszą cię, żebyś bisował (czyli powtórzył, chociaż najczęściej artyści na bis wykonują coś innego). Pamiętam, że do szkoły mogłem kiedyś podjechać tramwajem linii "15 bis" (z placu Zbawiciela w Warszawie na Bielany). "Dwojaki" to gliniane naczynia, mające dwie części - na zupę i drugie danie. Dwoisty Stawek jest w Dolinie Gąsienicowej, blisko schroniska Murowaniec, ale nie jest udostępniony ścieżką turystyczną. Można go zobaczyć z góry, z Kościelca.
Powiedzenie "dwa razy daje, kto szybko daje" ma dwa znaczenia, na dobrą sprawę przeciwne. Pierwsze: jeżeli szybko pomożesz, to jakbyś pomógł dwukrotnie. Drugie: nie spiesz się z ofertą, bo możesz stracić. Wreszcie, powiedzeniem o dwóch lewych rękach (bo to przecież określenie kogoś, kto np. nie umie prosto wbić gwoździa w deskę ani wkręcić śrubki) mogą czuć się dotknięci ludzie leworęczni. Jeszcze za czasów mojej młodości uważano to za wadę, którą należy zwalczać. Na szczęście to już minęło. W zapomnianej już gwarze warszawskiej "cwajnosem" nazywano buldoga (zwei to dwa po niemiecku).
Dla matematyka brydż jest grą dwuosobową (taką by była i piłka nożna, gdyby się zajmowali teorią futbolu!) - tu i tam są dwie partie, dwa zespoły. Dubeltówka zwana jest też dwururką - no, to widomo, ile ma luf. Pamiętasz pewnie, że z dwururki Jacek Soplica zastrzelił Stolnika. W biegach po zamkniętej pętli zawodnik jest zdublowany, jeżeli czołówka doścignie go "od tyłu". Filmowcy "kręcą dubla", gdy reżyser nie jest zadowolony z ujęcia. W czasach mojej młodości "dać dubla" znaczyło "przewrócić się do przodu" (synonim: "złapać zająca", natomiast upadek do tyłu określało się jako "wywinąć orła"). Chyba to przetrwało?
W trunku zwanym dwójniakiem na jedną część miodu przypada jedna część wody. Dwutakt w koszykówce to przepis, że można z piłką zrobić tylko dwa kroki. Nie należy go mylić z silnikiem dwusuwowym. Pierwszym samochodem całkowicie polskim (nie na żadnej licencji) była dwusuwowa Syrena, produkowana w latach 1957-1972. Nawet na owe czasy była dość toporna.
Odpowiedź na zadanie 2
Każda z figur z tego zadania ma dwie osie symetrii. Są one prostopadłe. Gdyby nie były, powstałaby i trzecia. Spójrz na rysunek 7. Załóżmy, że osiami symetrii są dwie proste ukośne. Zaczynamy np. od niebieskiej figury. Odbijamy ją w jednej i drugiej osi, powstaje czerwona i turkusowa. Czerwoną musimy odbić w drugiej osi - powstaje zielona. Z turkusowej - brązowa i musimy dodać różową (karminową) - jako odbicie brązowej. Pojawia się trzecia oś symetrii - pionowa. Ogólnie: odbicie jednej osi symetrii w drugiej daje trzecią. Tylko jeżeli osie wyjściowe są prostopadłe, to trzecia pokrywa się z pierwszą.
Komentarz do zadania 3
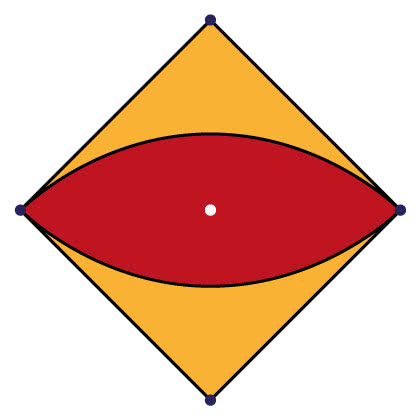
Ja nazwałby m dwukątem taką "soczewkę" (8), a nawet w prowadziłbym pojęcie dwukąta prostokątnego - widzimy go właśnie. A oto "zadanie w zadaniu": oblicz pole "dwukąta", jeżeli bok kwadratu ma długość a. Wskazówka: czy widzisz dwie ćwiartki koła?
Rozwiązanie zadania 4
Popatrzmy najpierw, co widać od razu. Liczba 22! ma 22 cyfry (wyliczone w tekście), a zatem 20! ma mniej cyfr. Przyjmijmy, że 20. Iloczyn 20!·22! ma zatem nie więcej niż 22+20=42 cyfry (tak naprawdę tylko 40).
Łatwo się przekonać, że 2022! ma tych cyfr znacznie więcej. Z całej silni weźmy tylko ostatnie 22 czynniki, czyli od 2001 do 2022. Każdy z nich jest większy od 103, a zatem ich iloczyn przekracza 1066.
2022! to iloczyn 2022 liczb po kolei, natomiast 20222022 to też iloczyn 2022 liczb, ale wszystkie są równe 2022. To znaczy, że 2022!<20222022, 20!·22!<20!22! Pozostaje umiejscowić liczbę 20!22!. Cóż to za olbrzymia liczba?
Jest to iloczyn 1 124 000 727 777 607 680 000 czynników, z których każdy ma nie mniej niż 20 cyfr. To jest właśnie największa liczba z podanych. Ma ona, bagatela, prawie kwadrylion cyfr.
Odpowiedź do zadania 6
Wszystkie małe trójkąciki mają tę samą podstawę i tę samą wysokość. Co do drugiego pytania zwróć uwagę, że zapytałem "ile widzisz" - a nie "ile jest"! Trochę żartobliwie, ale ponieważ na pytanie możesz odpowiedzieć byle co, na przykład siedemnaście i argumentować, że właśnie tyle widzisz. I wiesz, będziesz miał(a) rację! Nie będę mógł Cię przekonać, że widzisz więcej czy mniej. Dbaj zatem jasność wypowiedzi, a ja się wycofuję i zmieniam treść: ile trójkątów jest na tym rysunku? Powiem, ile ja widzę. Jeden trójkąt duży, w którym są wszystkie inne i drugi równoboczny, ten "nad kreską". W tym "nad kreską" mamy cztery trójkąty kolorowe: czerwony, turkusowy, żółty i zielony, ale jeszcze dwa prostokątne. "Pod kreską" mamy pięć trójkątów: żółty, turkusowy, niebieski, zielony i karminowy (w terminologii CMYK: magenta). Jest jeszcze kilka innych: turkusowo-niebieski, turkusowo-niebiesko-zielony, niebiesko-zielony. To nie wszystko: mamy po lewej żółto-czerwony… Dokończysz wyliczanie?
Rozwiązanie zadania 7 - a właściwie ogólniejszego
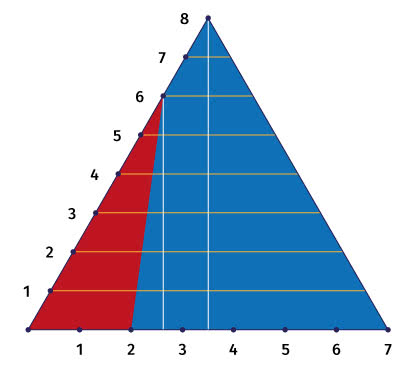
Niekiedy bywa tak, że łatwiej rozwiązać zadanie bardziej ogólne. Tak zróbmy i tutaj. Dzielimy jeden bok na m części, drugi na n. Łączymy punkt numer k na pierwszym boku z punktem numer l na drugim boku. Odcinamy trójkąt. Jakie jest jego pole w stosunku do pola całego trójkąta? Zadanie wygląda na skomplikowane, ale jest nietrudne. Nie siląc się na ogólność, podam rozwiązanie, gdy jeden z boków podzieliłem na 7 równych części, drugi na 8 i wziąłem trójkąt o wierzchołkach nr 2 i nr 6.
Odcięty trójkąt ma podstawę długości ![]()
wysokości "dużego" trójkąta. Jego pole jest zatem równe 
pola całego trójkąta.
Zrozumiałeś/aś? No, to narysuj sam/a.
Odpowiedź do zadania 8
Na przykład 4539281706·2=9078563412. Jak na to wpaść? Metodą prób i błędów, ale nie na oślep. Wybieramy najpierw takie liczby, żeby ich iloczyn przez 2 nie wyszedł poza 10. To są 4, 3, 2, 1, 0. Do każdej z nich dobieramy jedną z pozostałych, np. 45 39 28 17 06. Iloczyny tych grup przez 2 to 90 78 56 34 12. Zgadza się!
Ale przecież możemy te grupy przestawiać, np. 39 17 06 45 28 i też będzie dobrze (kto nie wierzy, niech sprawdzi). Pięć grup dwucyfrowych możemy ustawić na 5!=120 sposobów, z tym że musimy odrzucić 24 układy zaczynające się na 06. Mamy zatem co najmniej 96 rozwiązań zadania. Dlaczego "co najmniej"? To jasne - inny sposób może dać inne liczby!
Komentarz i rozwiązanie zadania 9
Mogło być na przykład tak. Bartek ma zdolności biznesowe i wzdłuż ulicy Głównej postawi kawiarnię, sklep spożywczy, a sam narożnik wydzierżawi na budkę z kebabem. Ania jest dentystką i woli mieć gabinet w spokojnym otoczeniu, z wejściem od ulicy Leśnej, z widokiem na drzewa. Może być też inaczej. Na działce od Głównej Anna stawia gabinet kosmetyczny, a Bartek, który jest naukowcem, potrzebuje ciszy i spokoju i mieszka w skromnym domku przy parku i lesie. A może znajdź inne zawody dla Anny i Bartka i zaproponuj im inny podział…
I tu jednak wkracza matematyka: jak podzielić coś, co nie ma obiektywnej, liczbowej wartości? A jak podzielić niepodzielne? Ale to temat na inny artykuł.
Michał Szurek