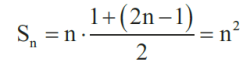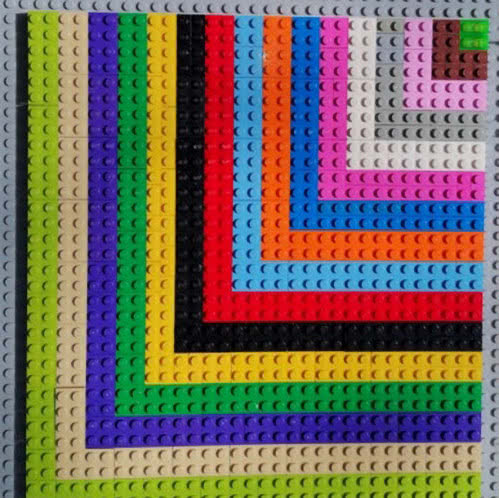Na cały nowy rok

Skupmy się jednak na matematyce. Czy liczba 2023 ma jakieś interesujące własności matematyczne? Trochę ich ma. Potraktujmy to jako przepowiednię: 2023 jest liczbą szczęśliwą. Tak jest. Przechodzi bezpiecznie przez "sito Józefa Flawiusza". Kim był Józef Flawiusz? W Wikipedii znajdziemy, że:
Józef Flawiusz (hebr. Josef ben Matatia, stgr. ᾿Ιώσηπος Φλαύιος, łac. Titus Flavius Iosephus, ur. 37, zm. po 94) - żydowski historyk pochodzący z rodu kapłańskiego - z klasy Joariba, pierwszej klasy kapłańskiej w Izraelu.
Brał udział w powstaniu żydowskim przeciw Rzymianom (rok 66 n.e.). Według anegdoty, został wraz z grupą 41 powstańców osaczony przez Rzymian w jaskini. Powstańcy nie chcieli się poddać, a ponieważ religia zabraniała samobójstwa, postanowili "odliczać" - ten, na kogo wskazała procedura, miał zabić poprzednika. Flawiusz z towarzyszem bezskutecznie chcieli odwieść ich od takiego rozwiązania. Wyliczyli zatem, gdzie sami powinni się ustawić, by być na końcu. Najwyraźniej im się to udało, bo potem Flawiusz zasłynął jako historyk i ogólnie intelektualista.
Już Eratostenes z Cyreny (276 - 194 p.n.e.) wiedział, jak otrzymywać liczby pierwsze. Należy "odsiewać" te pozostałe, czyli złożone. Z ciągu liczb naturalnych zostawiamy 2, a wykreślamy wszystkie inne parzyste. Najmniejszą nieskreśloną większą od 2 jest liczba 3. Zostawiamy ją, a wykreślamy wszystkie jej wielokrotności. Najmniejszą nieskreśloną większą od 3 jest 5. Zostawiamy ją i wykreślamy inne podzielne przez 5. Te, które "przeżyją" skreślanie - są liczbami pierwszymi - z wyjątkiem początkowej liczby 1, której nie uznajemy ani za liczbę pierwszą, ani za złożoną. Oto początek najsłynniejszego ciągu liczbowego w matematyce - ciągu liczb pierwszych. W pierwszej setce jest ich 25.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Prawie pół wieku temu odkryto zastosowania liczb pierwszych do kryptografii. W skrócie polega ono na tym, że rozkład dużych liczb na czynniki pierwsze jest zajęciem niesamowicie pracochłonnym. Mowa oczywiście nie o pracy z ołówkiem czy długopisem w ręku, tylko godzinach, dniach a nawet latach (!) pracy komputera. To tak, jak szukanie liścia w lesie - gorzej niż igły w stogu siana.
Sitem Flawiusza nazywamy w matematyce kilka algorytmów, polegających na podobnych operacjach. Najbardziej znaną i najbardziej pożyteczną jest wersja zaproponowana w 1955 roku przez Stanisława Ulama. Był to lwowski matematyk - wyjechał do USA w 1938 roku. Z racji swojego pochodzenia pewnie nie przeżyłby drugiej wojny światowej. W Stanach zasłynął ze swojego zaangażowania w projekt Manhattan. Kto z Czytelników nie wie, o co chodzi - zajrzyjcie, proszę, do Wikipedii. Ja nie chcę o tym pisać przy końcu roku 2022…
W procedurze Stanisława Ulama zaczynamy tak samo, od ciągu kolejnych liczb naturalnych. Musimy oczywiście ograniczyć się do pewnego ich zakresu, tysiąc, milion, sto milionów, kwadrylion.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, …, itd.
Skreślamy co drugą liczbę, zostają same nieparzyste. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, … itd.
Z nowego ciągu skreślamy co trzecią liczbę. Pozostaje:
1, 3, 7, 9, 13, 15, 19, 21, 25, 27, 31, 33, 37, 39, 43, 45, … itd.
Następnie usuwamy co czwartą, potem co piątą, co szóstą, co siódmą, ósmą i tak dalej aż do końca; oczywiście nie do końca wszystkich liczb (bo takiego końca nie ma). Przerywamy, gdy osiągniemy założony przedtem zasięg. Dla liczb, które zostały po tym wielokrotnym odsiewaniu, zaproponowano nazwę lucky numbers, liczby szczęśliwe. Oto początek ciągu liczb szczęśliwych. Widzimy, że na 51. miejscu znajduje się nadchodzący rok. Kolejnej liczby szczęśliwej nie dożyjemy: 2161.
1, 3, 7, 13, 19, 27, 39, 49, 63, 79, 91, 109,
133, 147, 181, 207, 223, 253, 289, 307, 349,
387, 399, 459, 481, 529, 567, 613, 649, 709,
763, 807, 843, 927, 949, 1009, 1093, 1111,
1189, 1261, 1321, 1359, 1471, 1483, 1579, 1693, 1719, 1807, 1899, 1933, 2023, …
Niestety, nazwa "liczby szczęśliwe" to właśnie tylko nazwa. Chciałbym móc wrócić do tego tematu za rok i mam nadzieję, że będzie nam to dane. 2024 też jest ciekawą liczbą - tyle pomarańczy wypełni piramidkę 22 piętrach…
Badania nad liczbami i ciągami liczbowymi są częściowo utajnione - właśnie z powodu zastosowań w kryptografii. Nie są to wyłącznie zainteresowania wojenne. Może to być zwykłe kodowanie, choćby na przykład podpis elektroniczny. Okazało się (co było niespodzianką dla matematyków), że "cudowne własności liczb pierwszych" pochodzą nie z samego ich określenia, a stąd, że można te liczby otrzymać metodą sita. Dlaczego zatem nie użyć innych sit? Może powstaną lepsze szyfry, a może po prostu utrudnimy zadanie hakerom, dając im jeszcze jedną barierę do pokonania: jakiego sita użyto. Może powstanie przysłowie: "obre sito to bezpieczne żyto"?
W matematyce liczby nieparzyste są ciekawsze niż parzyste. No bo przecież parzystą zawsze można podzielić przez 2 i dostaniemy…, albo parzystą, albo nieparzystą. Wiemy, że iloczyn liczb parzystych też jest liczbą parzystą. Można powiedzieć, że jest "podwójnie parzystą" - podzielną przez 4, taką bardziej złożoną. Nic podobnego nie ma miejsca dla liczb nieparzystych. Ułamek, którego licznik i mianownik są parzyste, można zawsze skrócić. Gdy są nieparzyste - można, ale nie zawsze.
W starożytności też przedkładano liczby nieparzyste nad parzyste. Jak powiedział Wergiliusz (poeta rzymski, Publius Verilius Maro, 78 p.n.e. - 19 p.n.e), Numero deus impare gaude. Bóg raduje się liczbą nieparzystą. Dziś jest różnie. Na ogół jednak parzystość jest w życiu codziennym odbierana jako coś pożądanego, nieparzystość jest dziwna i zła. Wyjątki są nieliczne: idąc z wizytą do znajomych, ofiarujemy pani domu trzy, pięć, siedem, dziewięć, może nawet siedemnaście kwiatów. Może być nawet efektowny jeden - ale nigdy dwa, cztery, sześć... Zwyczaj ten jest znany chyba tylko w Polsce; w każdym razie moi znajomi z różnych krajów bardzo dziwili się: co to za dziwny przesąd. A przecież po angielsku odd to dziwny, zaś odd number to liczba nieparzysta; po niemiecku liczby parzyste to gerade Zahlen (a więc "proste"), po ukraińsku mamy podobnie, jak w polskim, парне–непарне число. W polszczyźnie jeszcze w XVI wieku parzyste i nieparzyste to było cetno i licho. W pierwszej polskiej książce matematycznej (1538) Tomasz Kłos używa zabawnie dziś brzmiącego sformułowania przyszło w licho w znaczeniu otrzymaliśmy liczbę nieparzystą.
Komisje i komitety powinny składać się z nieparzystej liczby członków - wtedy nie ma kłopotu, co zrobić, gdy głosy układają się po równo. Przy okazji zwrócę uwagę na często popełniany błąd, że "bezwzględna większość" to 50% plus jeden głos. No, bo jak to będzie w komisji złożonej z trzech osób? Połowa to półtora głosu, a dodać jeden = 2 i pół głosu, czyli trzy! Dla komisji pięcioosobowej to znaczy 4:1.
Czy mieszkasz po parzystej, czy po nieparzystej stronie ulicy? Jakie zalety ma taka właśnie numeracja? O zaletach tych przekonałem się "na własnej skórze". Otóż w niektórych miastach niemieckich stosowano taki system: po jednej stronie ulicy szły numery po kolei, od 1 do, powiedzmy, 50, a od 51 do 100 wracały drugą stroną. Przyjechałem do Berlina późnym wieczorem. Mały, nieoświetlony podberliński hotelik był pod numerem 75, a zacząłem iść ulicą od numeru 1. Doszedłem do 50, a tu ulica się kończy. Muszę powiedzieć, że trochę zgłupiałem. A było to blisko słynnego muru berlińskiego, dzielącego miasto w latach 1961-1989.
Dużo liczb nieparzystych jest na korcie tenisowym. Każda połówka kortu (czyli pole jednego gracza) ma rozmiary 27 na 39 stóp. Siatka w środku ma wysokość 3 stóp (przy słupkach więcej), a grubość linii ma wynosić 3 cale. Pole serwisowe (tzw. karo) ma rozmiary 21 na 13,5 (stóp). Pamiętamy może, że 13 i 21 to kolejne liczby Fibonacciego, a ich stosunek jest dobrym przybliżeniem złotego podziału. Gracze zmieniają strony kortu po nieparzystej liczbie gemów (a więc i po pierwszym gemie każdego seta). Jest to sprawiedliwe - gdyby zmieniano po parzystej liczbie, każdy by serwował (w tenisie mówi się "podawał") zawsze z tej samej strony; na przykład pod słońce. Podobnie powinno być i w karnych w piłce nożnej, gdy w normalnym czasie jest remis: pierwsza drużyna strzela raz, potem każda na zmianę po dwa razy. Ale to by było zbyt skomplikowane dla kibiców.
W lipcu 2022 roku miałem zajęcia z dziećmi z Ukrainy. Zajęcia, organizowane przez Politechnikę Warszawską, miały dać dzieciom i ich rodzicom jakąś namiastkę normalnego życia. Zacząłem od takiego zadania:
Zadanie. Завдання. Narysuj 1+3+5+7+9. Narysuj 1+3+5+7+9+11.
Dzieci nie zrozumiały, choć bariera językowa nie była problemem. Jak to "narysować sumę liczb?" Pewna dziewczynka obliczyła w pamięci sumę, podeszła do tablicy i dwoma kolorowymi flamastrami narysowała ozdobne 25. Ale po dłuższej chwili wszyscy zorientowali się, o to chodzi. Dwoje innych uczestników jednocześnie wyrwało się do odpowiedzi, chłopiec narysował mniej więcej tak, jak na rysunku 2, dziewczyna, jak na rysunku 3.
Pochwaliłem i poprosiłem ich, by ustawili swoje kółeczka i odcinki w piramidkę. Zrozumieli słowo "piramidka" i domyślili się, o co mi chodzi. Chłopiec ustawił kółka ładnie, dziewięć na dole, wyżej siedem, potem pięć trzy i jedno. Dziewczynka zrobiła inaczej, ale właśnie tak chciałem.
Wyjąłem przygotowane grosiki (mam w domu dużo - właśnie do celów dydaktycznych) i każdy ułożył piramidkę, mniej więcej taką jak tę, którą narysował chłopiec.
"Pokażę wam jeszcze inny sposób układania liczb nieparzystych". Narysowałem tak (5). "Jak długie są kolejne korytarzyki?", zapytałem. Policzyli szybko, 1+3+5+7+9. "A jaką figurę wypełniają?" Najpierw nie rozumieli, co chodzi, ale miałem asystenta, studenta z Ukrainy. Gdy wytłumaczył im, o co chodzi, zrozumieli. Kwadrat po ukraińsku to kwadrat i wszystko było jasne. Trudności pojawiły się przy próbie zapisania tego wzorem i z tego zrezygnowałem, zadowalając się sformułowaniem, że w wyniku dodawania kolejnych liczb nieparzystych otrzymujemy zawsze liczbę kwadratową. Ale tu zapiszę:
1+3+5+…+(2n–1)=n²
Wróćmy do szkoły. Przypomnę standardowy, licealny, sposób obliczenia sumy 1+3+5+…+(2n–1). Mamy tu ciąg arytmetyczny o pierwszym wyrazie 1 i różnicy 2. Trochę kłopotu sprawia policzenie, ile jest składników. Liczba 1 to 2·1–1 , liczba 3 to 2·2–1 i tak dalej. Jest zatem n składników, a zatem
A dla maturzystów mam oczywiście zadanie: udowodnij wzór 1+3+5+…+(2n–1)=n² za pomocą indukcji matematycznej. Nie podam rozwiązania, to przecież standard.
Dodajmy więc liczby 1, 3, 5, 7, 9, 11. Otrzymamy 36. To ciekawa liczba. Jest zarówno kwadratem jak i (na dwa sposoby) trójkątem (6). Trzydzieści sześć kasztanów, orzechów albo monet można też ustawić w gwiazdę. Kolejne zadanie dla licealistów: ile kasztanów/monet/orzechów znajdzie się w gwieździe jak na rysunku 6 - tylko o ramionach (do gwiazdy pasuje raczej słowo "promień") długości n. To też nietrudne, a pouczające.
Wracam do zajęć z dziećmi. Następnym zadaniem było:
Ułóż 1+3+5+7+9+11 z trójkątnych klocków. Ułóż 1+3+5+7+9 z kwadratowych klocków.
Wyjąłem stosowne klocki i… miałem trudności z utrzymaniem porządku, bo wszyscy zajęli się budowaniem, niekoniecznie tego, co prosiłem. Ale w końcu powstały takie konstrukcje:
Gdzie są sumy liczb nieparzystych na fotografii 7? Duże trójkąty składają się z małych (takich, które widać w lewym górnym narożniku). Ile złączeń trzeba wykonać, by otrzymać duży trójkąt o podstawie długości n? Jednostką długości jest bok najmniejszego trójkącika.
Hitem zajęć okazała się zabawa klockami Lego. Zrobię tu dygresję. Wdrażamy dzieci do współzawodnictwa, walki o stopnie
i żeby być lepszym od innych. Cóż, tak bywa i w dorosłym życiu. Ale w Krajowym Funduszu na rzecz Dzieci, z którym związany jestem od ponad 30 lat, zwracamy uwagę na teamwork, nie współzawodnictwo, a współpracę. Udało mi się zorganizować takie kolektywne układanie mozaiki (8), na której najlepiej widać, że suma kolejnych liczb nieparzystych jest kwadratem liczby naturalnej. Było to trudne, zwłaszcza przy niełatwej komunikacji językowej. Potem zajęcia już się "rozeszły" - każdy budował to, co chciał. Ale trochę matematyki udało mi się przekazać.
Na zakończenie kilka słów o wspomnianym przeze mnie Krajowym Funduszu na rzecz Dzieci. Od 40 lat daje on tak zwane stypendia dla uczniów, którzy nie tylko zdolnościami wykraczają ponad przeciętną, ale także (co jest ważne) mają jakieś szczególne zainteresowania, pasje, którzy rozglądają się uważnie po tym, co dookoła. Dlaczego są to tylko "tak zwane" stypendia? Dlatego, że nie dajemy pieniędzy do ręki, ale organizujemy bezpłatne zajęcia, warsztaty, staże i obozy naukowe. Fundusz współpracuje z najlepszymi szkołami wyższymi. Interesujemy się naszymi podopiecznymi przez wiele lat. Sporo z nich wraca do Funduszu już jako profesorowie uniwersytetów. Zachęcam młodzież do przysłania swojego zgłoszenia. Oczywiście wszelkie informacje - również wymagania - da się znaleźć w Internecie.
Michał Szurek