Krzywe, krzywki i krzywiki

Potrzebowałem w związku z tymi zajęciami trochę klasycznych przyborów szkolnych: linijki, ekierki, cyrkle. Znalazłem wszystko w lokalnym sklepiku, jeszcze nie przejętym przez duże sieci handlowe - ale nagle zobaczyłem na półce coś, co momentalnie przypomniało mi dość dawno minioną młodość: komplet krzywików - czyli takich zakrzywionych linijek, do rysowania na brystolu, tuszem. Natychmiast kupiłem. Stoją sobie teraz na półce, jak fotografia z tamtych lat.
Lubię takie stare przyrządy. Mam w domu kilka "wiecznych piór" - obecnie są to dość drogie gadżety. Mam także i coś, co za moich szkolnych czasów nazywało się "zwykłym piórem" - w obsadkę wkładało się stalówkę. Maczało się ją w kałamarzu z atramentem, a ewentualne kleksy wysuszało bibułą. Najpopularniejszą stalówką była "krzyżówka" - "serek" był delikatny i dawał cienkie litery, a "rondówka" służyła do pisma technicznego. Droga młodzieży: ile to nowych słów poznaliście tu, w tym jednym akapicie!
Ogólnie, krzywiki to szablony używane do wykonywania rysunków technicznych przy wykreślaniu linii krzywych. Użycie krzywika pozwala na wyprowadzenie dowolnej linii krzywej o zmiennym przebiegu, która nie jest łukiem okręgu. Praca z krzywikiem polega na połączeniu kolejnych punktów z zachowaniem płynnego przebiegu linii, co jest możliwe do osiągnięcia przy pokrywaniu się końcowych odcinków krzywej dla każdego kolejnego przyłożenia szablonu. Krzywiki jeszcze nie podzieliły losu zapomnianego już całkiem suwaka logarytmicznego - kalkulatora sprzed ponad pół wieku. Suwak też jeszcze mam, bardzo zużyty.
Moje krzywiki sprzed sześciu dekad (!) były wykonane z cieniutkiej dykty. Te, które kupiłem teraz za 6 złotych, są oczywiście plastikowe. Niezmienny pozostał kształt. Wiem, że takie same krzywiki były w użyciu jeszcze w latach trzydziestych XX wieku. Ciekawe, kto je wymyślił i może opatentował. Szukałem tej wiadomości w Internecie, ale nie znalazłem. Oto mój nowy komplet: po lewej krzywik paraboliczny, po prawej u góry eliptyczny, u dołu hiperboliczny.
Zmieniłem przygotowany temat zajęć i postanowiłem opowiedzieć młodzieży o różnych krzywych, począwszy od stożkowych. To jest wspólna nazwa elips, parabol i hiperbol. Już starożytni dobre je znali. Apoloniusz z Pergi (260 p.ne. - ok. 200 p.n.e.) napisał obszerny traktat o nich.
Ale najpierw porozmawialiśmy o … figurach stylistycznych. Odpytałem uczniów z wiadomości, które zdobywają na lekcjach języka polskiego. Ucieszyłem się, bo wiedzieli, o co chodzi. Przypomnę Czytelnikom. Elipsa nazywana jest też wyrzutnią, bo właśnie tak działa - możemy wyrzucać zbędne słowa, skracać wypowiedzi, zachowując sens. Na przykład zamiast "czy właśnie pada u nas deszcz?" wystarczy krótkie "pada?". Rozumiemy, że nie chodzi o to, czy na Antarktydzie pada śnieg, tylko deszcz w naszym mieście. A w matematyce obiekty eliptyczne są zwykle ograniczone i zwarte. Z hiperbolą mamy do czynienia, gdy coś wyolbrzymiamy - albo świadomie zmniejszamy: "morze łez", "bezkresne lasy", "chudy jak palec", "mały jak mrówka", czy "powódź światła" (to ostatnie jest także ciekawym środkiem stylistycznym, zwanym synestezją - polecam wygooglać sobie!). Ileż to razy mówimy na powitanie: "bardzo mi przyjemnie", choć czujemy obojętność… Obiekt lecący z prędkością hiperboliczną może pochodzić spoza Układu Słonecznego. Taki właśnie statek kosmiczny napotkał pilot Pirx w jednym z opowiadań Stanisława Lema. Wreszcie parabola - najbardziej tajemnicza z trójki. Znów przywołam Lema. Czytając jego opowiadania o dalekich światach i tajemniczych kosmitach, czujemy, że to tylko parabola - bo naprawdę chodzi o nas, o nasz świat, o nas samych. Mały Książę, Kubuś Puchatek zawierają mnóstwo parabol. Niemal każda opowieść biblijna jest paraboliczna, jak na przykład historia o marnotrawnym synu, powracającemu do domu ojca, po roztrwonieniu majątku.
Grecy znali dużo krzywych. Brały one początek z konstrukcji powabnych matematycznie. Podstawowe i najpiękniejsze były linie proste i okręgi oraz ich pochodne, jak cykloida, epicykloidy, hipocykloidy i spirale. Uznawanymi narzędziami do rysowania były tylko liniały (linijki) i cyrkle. Wszystko to odbiło się na kosmologii. W stworzonym przez Greków systemie świata (kojarzonym zwykle z imieniem Ptolemeusza, II wiek n.e.) Słońce, Księżyc i planety krążyły wokół nieruchomej Ziemi. Nie zgadzało się to wystarczająco dokładnie z obserwacjami, zatem z czasem rozbudowano system, dopuszczając okręgi toczące się po innych okręgach. Wszystkich tych okręgów u Ptolemeusza było aż 41. Dla wyjaśnienia skomplikowanego ruchu planet na sferze niebieskiej (niekiedy jest ruch wsteczny, planeta jak gdyby zawraca na niebie), a szczególnie zakreślania przez nie pętli, Ptolemeusz przyjął założenie, że po kołowej orbicie ekscentrycznej - zwanej deferentem - porusza się ruchem jednostajnym nie sama planeta, ale środek innego, mniejszego koła zwanego epicyklem, a dopiero po obwodzie epicyklu porusza się ruchem jednostajnym sama planeta. Stąd nazwa "epicykloida" na określenie krzywej powstającej przez toczenie się okręgu po zewnętrzu innego.
Przechodziłem wojskowe szkolenie studentów. Z budowy armaty zapamiętałem dużą liczbę krzywek - po których obracały się koła, lufa i pokrętła. Myślałem, że zaprojektowanie dobrej krzywki jest bardzo trudne. Nie myliłem się.
Ale przejdźmy do konkretnej, łatwej matematyki. Elipsę znamy wszyscy. Widzimy ją na co dzień - gdy oglądamy cień koła, albo gdy patrzymy na nie z boku (2). Ciekawe, że kulę zawsze widzimy jako kulę (ściśle rzecz biorąc, koło) - ale to dlatego, że nie możemy na nią spojrzeć z punktu … w przestrzeni czterowymiarowej.
Zwróciłem kiedyś uwagę na elipsę na chodniku, (3). Dawno nie widziałem eliptycznego pudełka z rybkami, ale doskonale pamiętam, że były.
Odkrycie, że planety krążą po elipsach wokół Słońca, przypisujemy niemieckiemu uczonemu, Johannesowi Keplerowi (1557–1630). Według legendy, do tego samego wniosku doszła w V wieku Hypatia z Aleksandrii, jedna z niewielu kobiet tamtych czasów, które znamy z imienia. Była niezłą matematyczką i astronomką. Jak to często bywało, w końcu oskarżono ją o bezeceństwa i zamordowano. Pomysł palenia czarownic na stosie jest późniejszy.
Jan z Nikiu, koptyjski kronikarz z VII wieku napisał:
Kobieta filozof, poganka imieniem Hypatia, cały czas poświęcała się magii, astrolabiom i instrumentom muzycznym, swymi satanicznymi sztuczkami zwiodła wielu ludzi. Gubernator miasta świadczył jej niezwykłe honory, gdyż go zaczarowała. W wyniku tego przestał chodzić do kościoła, jak miał w zwyczaju.
W nastrojowym filmie o Hypatii, Agora (2009, reż. Alejandro Amenábar), główną rolę gra Rachel Weisz. Hypatia przeżywa tortury umysłu, gdy dochodzi do wniosku, że Ziemia musi się poruszać po okręgu, który ma dwa środki. Tak, po okręgu, który ma dwa środki.
Zanim zaczęliśmy (na lekcji, druga klasa liceum) przyglądać się elipsie, rzuciłem takie właśnie pytanie: czy to się da jakoś zrozumieć, czy może być coś takiego, jak okrąg o dwóch środkach. Wywołało to skojarzenie z cielęciem z dwiema głowami, ale po krótkim czasie zaczęliśmy się zastanawiać. Okrąg o dwóch środkach? Pozornie bez sensu, ale pomyślmy. Skoro okrąg składa się z punktów tak samo oddalonych od środka, to jeżeli mają być dwa środki, to by znaczyło, że są to punkty tak samo odległe od nich. "To na pewno nie o to chodzi - takie coś nazywa się symetralną odcinka" powiedziałem.
Ktoś rzucił pomysł: a może tak: kiedy podróżujemy od środka zwykłego okręgu do brzegu (wzdłuż promienia), a potem z powrotem, to przebędziemy drogę długości dwóch promieni. Co zrobić, jeżeli będą dwa środki? To proste: droga od jednego środka do obwodu i potem do drugiego "środka" ma być taka sama, niezależnie do którego punktu obwodu się udamy.
Być może uczeń ten wiedział już coś o elipsie, ale właśnie o to mi chodziło. Sprecyzowałem:
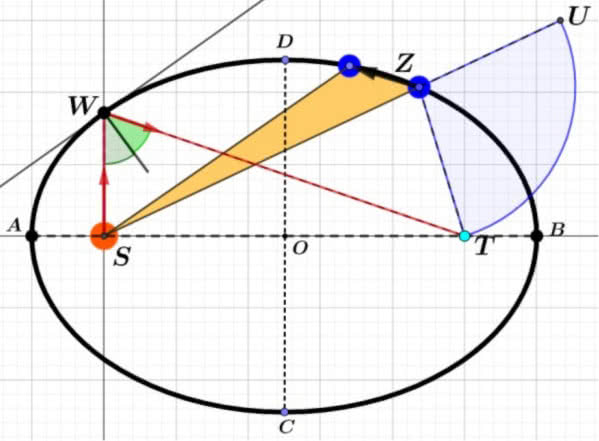
Elipsa jest krzywą, która ma dwa ogniska. Suma odległości każdego punktu elipsy od ognisk jest stała. Sprawdziliśmy, że tak jest (5), po prostu mierząc odległości cyrklem. Ogniska tam - to punkty S i T. Suma odległości każdego punktu elipsy od jej ognisk jest stała; na rysunku mamy SZ+ZT=SW+WT=SA+SB=AB.
Przyjrzyjmy się dokładniej rysunkowi 5. Pokazuje najważniejsze własności elipsy. Elipsa ma oś wielką i małą, na rysunku to AB i CD. Stosunek odległości między ogniskami do długości wielkiej osi nazywamy mimośrodem. Jest on dobrą miarą spłaszczenia elipsy. Zobaczmy: okrąg ma jeden środek, czyli dwa takie same ogniska. Odległość między nimi jest wobec tego równa zero, a zatem okrąg ma mimośród zero - jego spłaszczenie jest zerowe. Elipsa na rysunku 5 ma mimośród 5:7 czyli w przybliżeniu 0,714.
Promień wysłany z jednego ogniska elipsy odbija się od niej i dociera do drugiego - każdy w tym samym czasie. Na rysunku 5 widzimy, że kąt padania promienia w punkcie W jest równy kątowi odbicia. Teoretycznie więc można zapalić przedmiot znajdujący się w punkcie T, rozpalając ogień w S. To tylko teoretycznie, ale podobno jednak już w starożytności potrafiono konstruować takie sale, żeby słowa wypowiedziane w jednym końcu były dobrze słyszalne w drugim. Tymi końcami musiały być ogniska pewnej elipsy.
Na rysunku mamy jeszcze Słońce S i Ziemię Z. Drugie prawo Keplera mówi, że planety poruszają się po orbitach tak, że w równych odstępach czasu zakreślają równe pola (żółty trójkąt na rysunku 5). Punkt, w którym jesteśmy najbliżej Słońca nazywa się aphelium, ten najbardziej oddalony - perihelium. Przez analogię mamy apogeum i perigeum. Księżyc w swoim apogeum oddalony jest od Ziemi o 406700 km, a w perigeum 365500 km. W mowie potocznej używamy niekiedy słowa apogeum - mniej więcej w znaczeniu 'największe spiętrzenie, sytuacja ekstremalna'. Jeszcze niedawno zastanawialiśmy się, kiedy nadejdzie apogeum pandemii. Teraz boimy się, czekając na apogeum inflacji.
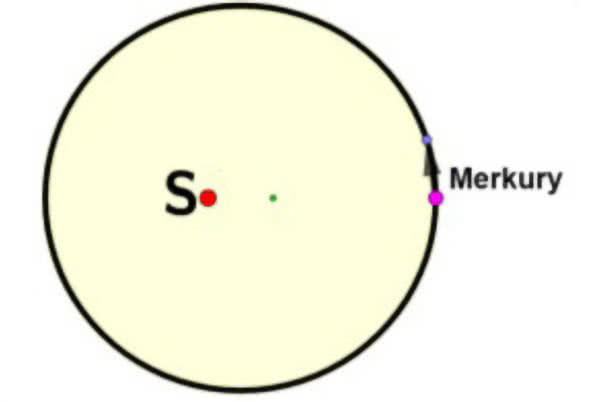
Orbita Ziemi jest niemal kołowa - jej mimośród to tylko 0,0167. Spośród planet najbardziej wydłużoną orbitę ma Merkury - jej mimośród to 0,2056. Orbita Neptuna jest już "bardzo kołowa", bo ma mimośród tylko 0,0086.
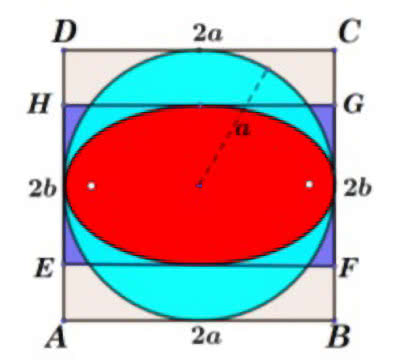
Obliczenie pola ograniczone elipsą nie jest bardzo trudne. Wystarczy obliczyć prostą całkę, ale można tego uniknąć sprytnym rozumowaniem. Można powiedzieć, że elipsa powstaje z okręgu przez ściśnięcie w jednym kierunku (8). Fachowo nazywa się to powinowactwo osiowe. Pół wieku temu uczono o tym w liceach, ale to sa ne vrati. Tym niemniej spójrzmy na rysunku 8. Gdy ściśniemy kwadrat ABCD do prostokąta EFGH, pole kwadratu zmniejszy się z 4a2 do pola prostokąta 4ab. Można oczekiwać, że to samo zajdzie dla koła i elipsy. Pole koła na rys. 8 to πa2 , zatem pole elipsy to πab. I to jest właściwa odpowiedź.
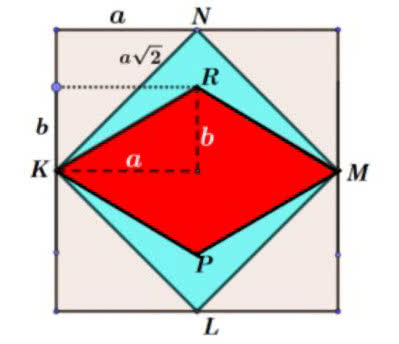
Napisałem, że to rozumowanie jest "sprytne". Daje poprawny wynik - ale dotyczy tylko pola, a nie np. obwodu. Zobaczmy: obwód prostokąta ABCD jest równy 8a, natomiast dla "ściśniętego" prostokąta otrzymamy 4a+4b. Rządzi tym jakaś inna zasada, trudna do odgadnięcia. Widać to dobrze na przykładzie dwóch rombów (9). Pole rombu KLMN jest równe 2a2 (jest on zresztą kwadratem), pole "ściśniętego", to jest KPMR wynosi 2ab. Stosunek jak dla elips, ale dla obwodów jest jeszcze inaczej. Obwód kwadratu KLMN to 2a√2, natomiast obwód ściśniętego rombu KPMR jest równy 4√a2 +b2 . Nie powinno nas dziwić, że jest inaczej dla obwodu, niż dla pola. Co innego jest ściskać jakąś powierzchnię, co innego nitkę.
I tu dochodzimy do właściwości, którą z początku trudno pojąć. Francuski matematyk Joseph Liuoville (1809–1882) wykazał, że długości łuku elipsy nie da się dokładnie obliczyć. Wygląda to z jednej strony smutno, a z drugiej niezrozumiale. Jak to "nie da się?" Sprawa jest jednak prosta. Przecież nawet obwodu koła "nie da się" dokładnie obliczyć, bo znanym wszystkim wzorze występuje "nieobliczalna" liczba π. Możemy ją przedstawić praktycznie z taką dokładnością, jak chcemy - ale tylko w przybliżeniu. Z elipsą jest jeszcze gorzej - odpowiednich całek nie da się wyrazić przez znane nam funkcje. To też nie powinno nas dziwić. Przecież dobrze znana funkcja "sinus" też kiedyś była dla nas nowa, niesprowadzalna do przedtem znanych. Wartości sinusa też znamy w przybliżeniu.
To, co nie jest problemem inżynierskim (zawsze przecież można wziąć lepsze przybliżenie), jest ważne gdzie indziej, na przykład przy konstrukcji… doskonałych szyfrów. Ale to już inna historia.
Na lekcji w szkole w Piastowie zorientowałem się w tym momencie, że uczniowie przestają już rozumieć. Na szczęście rozległ się dzwonek. Do elipsy i innych krzywych wróciłem po tygodniu… Rysowaliśmy cissoidę i konchoidę.
Michał Szurek