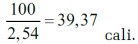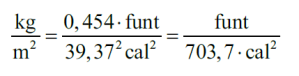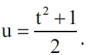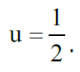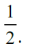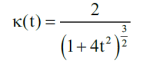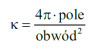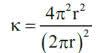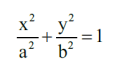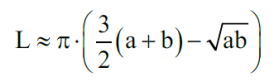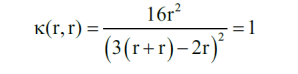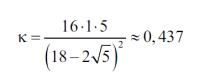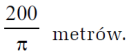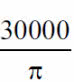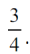Lekcje piastowskie. Matematyka okrągłości
Od uczniów w LO w Piastowie dowiedziałem się, że na lekcjach biologii nauczycielka omówiła popularny od pewnego czasu "wskaźnik otyłości" BMI.
Podobno teraz w szkołach bardzo dużo uczniów chce być zwolnionym z lekcji wychowania fizycznego. Nie będę tego komentował, powiem tylko, że na obozach naukowych Funduszu (o którym wspomniałem), codzienne zajęcia sportowe są obowiązkowe.
Nie jest bezwzględną prawdą, że im kto chudszy, tym zdrowszy. Jednak o medycynie nie będę się tu wypowiadał - zwyczajnie, z braku kompetencji. Ograniczę się do bezpiecznego obszaru - do matematyki.
Otóż wskaźnik BMI wymyślił już w 1832 roku belgijski matematyk Adolf Quetelet. W 1972 roku formułę odkrył na nowo - a może dotarł do badań Queteleta - amerykański fizjolog Ancel Keys. Od niego pochodzi nazwa i skrót: BMI, Body Mass Index, co można tłumaczyć się na polski jako "wskaźnik masy ciała". Wzór jest podejrzanie prosty:
Wagę wyrażamy w kilogramach, wzrost w metrach. Obliczmy ten wskaźnik dla hiszpańskiego tenisisty Rafaela Nadala. Według Wikipedii, ma on 185 cm wzrostu i 85 kg wagi. Podzielmy:
Jest to wskaźnik na granicy nadwagi (którą BMI ustala na 25). Kto widział Nadala w telewizji, może się zdziwić. Sprawdziłem też chudego jak "śmierć na chorągwi" Nowaka Djokowica, obecnego lidera rankingu na najlepszego tenisistę. U niego wychodzi 22, w środku normalności. Fanom piłki nożnej polecam sprawdzić, czy znany piłkarz Robert Lewandowski nie jest przypadkiem zbyt gruby. Wzrost i wagę tego piłkarza można znaleźć w Internecie. Ogólnie nie jestem zwolennikiem "spiskowej teorii dziejów", ale nie odrzucałbym hipotezy, że takie a nie inne ustawienie poziomów normalności odbyło się pod presją firm farmaceutycznych (oczekujący zysków z kuracji odchudzających).
Tak czy owak, jak każda zbyt uniwersalna formuła matematyczna, tak wzór BMI ma ograniczoną stosowalność, ponieważ nie uwzględnia wielu naszych uwarunkowań. Tak, że jeżeli droga Czytelniczko, drogi Czytelniku masz za duże BMI, to może nie twoja wina, tylko… matematyki. Matematyka jest piękną nauką, ale i niebezpiecznym narzędziem, jeżeli stosowana bez należytej refleksji. Ciekawe jest też umieszczenie w mianowniku BMI drugiej potęgi wzrostu. To znaczy, że traktujemy człowieka jak istotę płaską, dwuwymiarową. Dziwne, ale podobno mimo swoich wad, wskaźnik ten sprawdza się w miarę dobrze.
Zadanie. Wyraź formułę na BMI, gdy wagę podajemy w funtach, a wzrost w calach.
Jest to dobre zadanie na ogólną orientację w prostej, codziennej matematyce. Polecam nauczycielom. Pamiętam, że przeliczanie jednostek sprawiało kłopot nadzwyczaj wielu studentom pewnego wydziału Uniwersytetu Warszawskiego. Rzecz jasna, nie był to wydział matematyczny.
Rozwiążę. Funt to 0,454 kg. Pamiętam z dzieciństwa, że gdy poprosiło się w sklepie o "pół funta masła", to ekspedientka wiedziała, o co chodzi. W Niemczech do tej pory rozumieją. Cal to 2,54 cm, a więc metr to
Jak przeliczyć jednostki? Mamy taką zależność:
Wynika stąd, że "funtowo-calowe" BMI trzeba pomnożyć przez 703,7, żeby dostać "metrowo-kilogramowe".
***
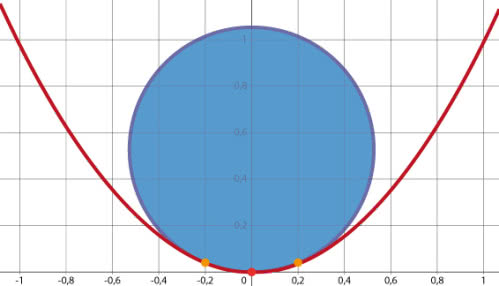
W geometrii badamy krzywiznę i zaokrąglenia. Jak bardzo zakrzywiona jest linia? Jak to zmierzyć? Odpowiedź zna każdy kierowca. Na każdym łuku szosy musimy obrócić kierownicę, żeby skręcić nie za dużo, nie za mało. Moglibyśmy mierzyć krzywiznę toru jazdy jako miarę kąta, o jaki skręcamy kierownicę. To byłoby niepraktyczne, ale sam pomysł jest dobry. Krzywiznę linii w danym punkcie mierzymy promieniem okręgu najlepiej pasującym do tej krzywej w tym punkcie. Można zapytać, co to znaczy: "najlepiej pasujący". Odpowiedni wzór jest skomplikowany, ale da się zrozumieć tak. Wyjaśnię na przykładzie paraboli. Chcę zmierzyć jej krzywiznę w wierzchołku - a więc dopasować do niej jak najściślej okrąg przechodzący przez wierzchołek. Bez wzorów i obliczeń się raczej nie da. Parabola będzie opisana równaniem y=x2 (1). Pamiętamy ze szkoły, prawda?
Wybiorę dwa punkty na paraboli, bliskie wierzchołka, powiedzmy (t, t2) i (–t, t2), gdzie t jest jakąś małą liczbą. Wyznaczę okrąg przechodzący przez te dwa punkty i przez wierzchołek paraboli. Do określenia krzywizny potrzebny będzie promień tego okręgu. Jego środek jest w punkcie na osi pionowej, niech to będzie punkt (u, 0). Promień okręgu jest równy u, ale jest równy też odległości punktów (u, 0) i (t, t2). Obliczając te odległości, otrzymamy
To jest promień okręgu przechodzącego przez wybrane dwa punkty paraboli i przez jej wierzchołek.
Dla t=1 dostajemy
Najlepiej pasujący okrąg do paraboli w jej wierzchołku ma promień
Ponieważ krzywiznę określamy jako odwrotność promienia tego najlepiej pasującego okręgu, więc obliczyliśmy, że krzywizna paraboli w jej wierzchołku jest równa 2.
***
Nie ma tu miejsca na wycieczkę w przestrzeń i teorię jej zakrzywienia, choć pewnie każdy słyszał "zakrzywieniu przestrzeni" i o zagadnieniu kosmologicznym, czy i jak nasz Wszechświat jest zakrzywiony. Z powierzchniami stykamy się na co dzień, zakrzywienie całej przestrzeni trudno sobie wyobrazić, ale stosunkowo łatwo opisać matematycznie. To jednak temat na inną lekcję. Znów muszę się "przywołać do porządku" i wrócić do prostej matematyki.
Każdy się zgodzi, że okrąg (czyli brzeg koła) jest tak samo zakrzywiony w każdym punkcie. Koło jest idealnie okrągłe. Okrąglutkie na 100%. Czy można w procentach wymierzyć okrągłość figury?
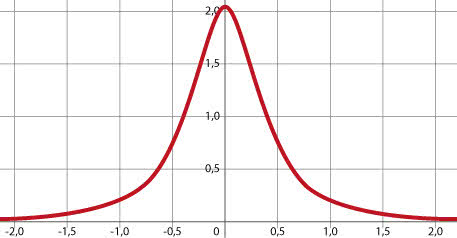
Można, i to na kilka sposobów. Dają one różne wyniki, bo samo pytanie nie jest precyzyjnie postawione. Nie ma w nim jasnego określenia, co to jest okrągłość. Odpowiedź na to pytanie to właściwie już podanie sposobu pomiaru. Można postąpić tak: zobaczyć, jak szybko zmienia się krzywizna danej linii. Dla okręgu będzie to funkcja stała, dla paraboli - co nie tak trudno wyliczyć - krzywizna wyraża się wyglądającym skomplikowanie wzorem:
Nietrudno narysować wykres tej funkcji (2).
***
Prostszą "miarę okrągłości" otrzymujemy przyrównując figury do koła w inny sposób. Wykorzystujemy izoperymetryczną własność okręgu. To długie słowo "izoperymetria" wyjaśnia się prosto. Chodzi o to, że okrąg otacza jak największe pole ze wszystkich figur o tym samym obwodzie. Przyjmujemy zatem miarę okrągłości figury jako współczynnik:
Czemu tak dziwnie? Zobaczmy. Jak okrągły jest okrąg (czyli brzeg koła)? Oczywiście doskonale okrągły, na 100%. Wyliczmy. Pole koła to πr2, obwód to 2πr, a więc
wynosi 1, czyli 100%. Zgadza się - współczynnik 4π w liczniku był potrzebny, by wynik pomiaru zgadzał się ze zdrowym rozsądkiem. Tylko dla okręgu współczynnik ten jest równy 1. Dla pozostałych figur wychodzi mniej.
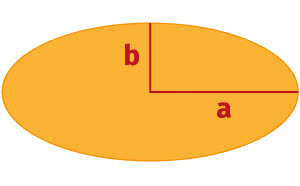
Każdy widział elipsę; można ją najprościej opisać jako spłaszczone koło. Gdy spojrzymy na zdjęcie stadionu piłkarskiego z trybun, zobaczymy eliptycznie spłaszczone koło środkowe, a gdy w programie graficznym Paint narysujemy koło i spłaszczymy je odpowiednio przeciągając myszką, otrzymamy właśnie elipsę.
Równaniem elipsy we współrzędnych kartezjańskich jest:
Liczby a, b to długości półosi elipsy. Gdy długości osi są równe, elipsa staje się okręgiem (3).
Do badania okrągłości elips użyjemy wzorów na pole i obwód elipsy. Z polem jest stosunkowo łatwo: pole elipsy (ściśle: pole obszaru ograniczonego przez elipsę półosiach a, b) jest równe S=π·ab. Natomiast obwód elipsy wyraża się skomplikowanymi całkami (zwanych dlatego całkami eliptycznymi), ale bardzo dobre do naszych celów jest przybliżenie
Wynika stąd wzór na miarę okrągłości dla elipsy półosiach a, b:

Sprawdźmy najpierw, co dla okręgu. Półosie są równe promieniowi, czyli a=b=r i mamy
Zgadza się z tym, co było przedtem - okrąg jest okrągły na 100%.
Obliczymy okrągłości różnych elips. Przekonamy się, że nasza miara dobrze oddaje intuicyjny sens tego pojęcia: im coś bardziej zbliżone do koła, tym większy ma współczynnik "okrągłości". Zobaczmy, jak to jest dla najbardziej spłaszczonej elipsy (żółtej na rysunku 4). Długości jej półosi to 1 i 5. Podstawiamy do wzoru na okrągłość elipsy:
To i tak dość dużo, prawie 48%. Tak jednak działa nasza miara.
Wspomnę o ciekawym trójkącie krzywoliniowym. Otóż okrąg (albo koło) jest figurą o stałej szerokości - może toczyć się między dwiema równoległymi prostymi. Jest zaskoczeniem dla każdego, kto widzi to po raz pierwszy, że są i inne krzywe o stałej szerokości, najbardziej znaną widzimy na rysunku Taki trójkąt o zaokrąglonych bokach nazywa się trójkątem Reuleuax (5). Jechać na rowerze o takich kołach dało by się "bardzo od biedy" - okropnie by szarpało w przód i w tył. Natomiast ma ten trójkąt inne zastosowania. Po pierwsze, został zastosowany w alternatywnym silniku samochodowym - silniku Wankla. Po drugie - wiertłem w takim kształcie da się wiercić kwadratowe otwory. Polecam obejrzeć w Wikipedii; wrażenie jest duże. Nietrudno obliczyć okrągłość takiego trójkąta: 89,7%.
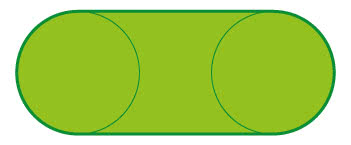
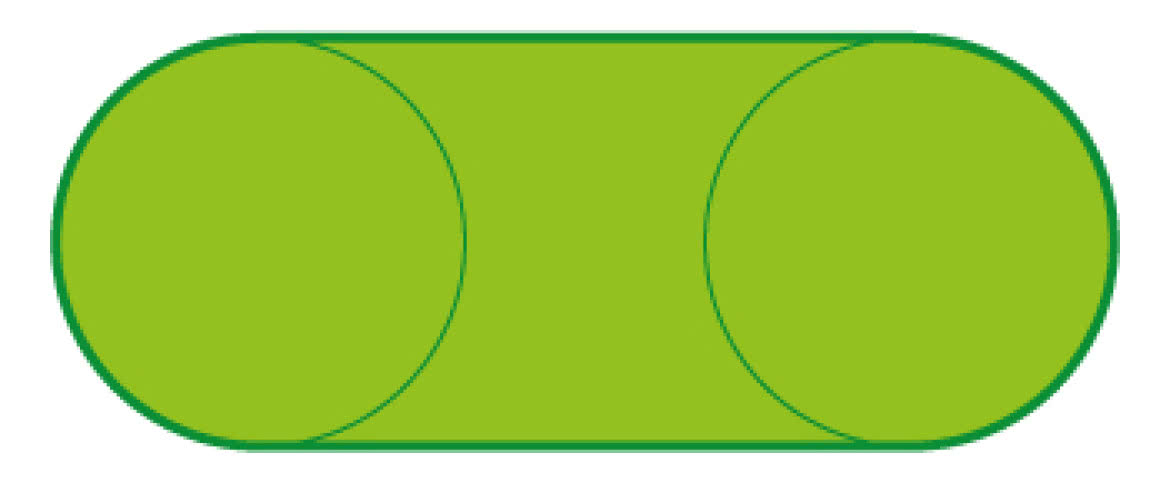
Zaciekawiło mnie, ile wynosi miara okrągłości stadionu lekkoatletycznego. Jak wiemy, ma on obwód 400 metrów, a przepisy IAAF precyzują, że zarówno łuki, jak i odcinki proste powinny mieć po 100 metrów (6).
Łuki kół mają zatem promień
metrów, a zatem prostokąt wpisany w stadion ma rozmiary 100 na
Obliczamy stąd łatwo, że pole powierzchni stadionu jest równe
metrów kwadratowych, a stąd wynika ciekawie wyglądający wynik:
Okrągłość stadionu lekkoatletycznego to dokładnie 75%. Nie sądzę, by 120 lat temu, kiedy tworzono zasady sportu, ktoś zastanowił się: jakie przepisy narzucić, żeby biegacze rywalizowali na obiekcie okrągłym na trzy czwarte. Natomiast przy tworzeniu tabel dla zawodów w dziesięcioboju najwyraźniej zatrudniono statystyka. O tym innym razem. Matematyka w sporcie to nie tylko obliczanie, kto kiedy wpisał się na listę strzelców.
Michał Szurek