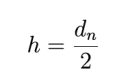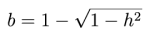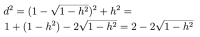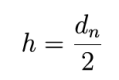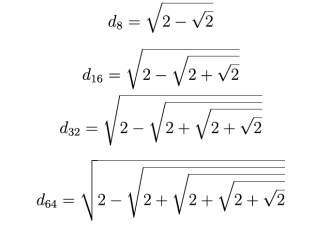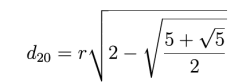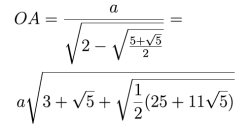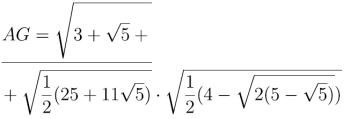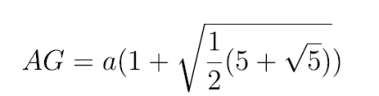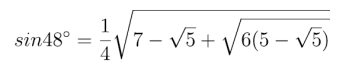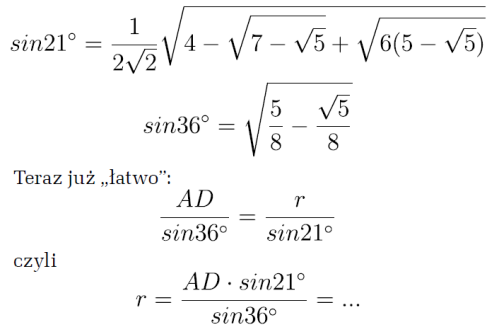Felga z Bielska i powrót do przeszłości
Ruszają w dal pociągi dwa,
z miasteczka B do miasta A
i z miasta A do miasta B
i mam określić, gdzie spotkają się.
Ich prędkość znam, odległość znam
i wszystko wyznaczone mam.
Lecz to zadanie peszy mnie
I profesora oko złe.
Z piosenki w wykonaniu Grażyny Świtały
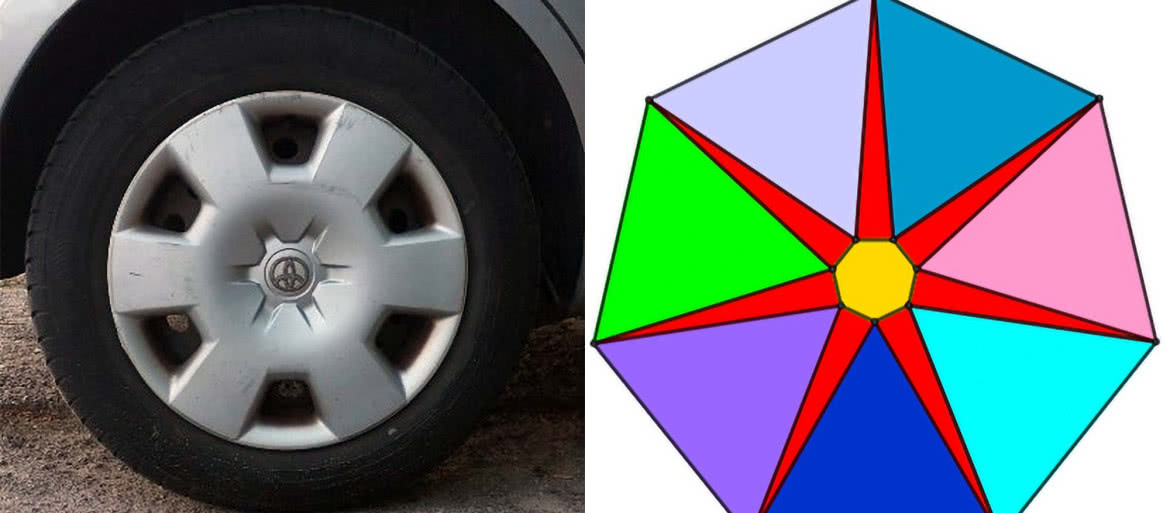
Kontynuowałem swoje małe hobby - przypatrywanie się felgom samochodowym i szukaniu w nich interesującej geometrii. Na pierwszych trzech zdjęciach widzimy „klasykę gatunku” - proste felgi o symetrii pięciokątnej, sześciokątnej i siedmiokątnej. Te ostatnie są rzadziej spotykane, ale nie dlatego, że siedmiokąt foremny nie jest - matematycznie rzecz biorąc - konstruowalny. To może wzbudzić zdziwienie: jak to, przecież właśnie widzimy, że jest. Dla tych Czytelników, którzy byli uczniami jeszcze 30 lat temu, ta pozorna sprzeczność będzie zrozumiała. Dla pozostałych - wyjaśnię przy końcu.
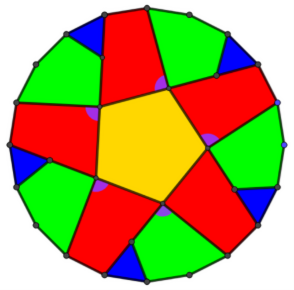
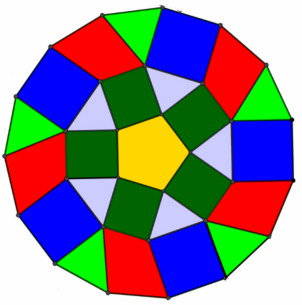
Aha. Na ogół nie są to felgi, tylko plastikowe kołpaki, nałożone na nie. Ale dla prostoty będę je felgami. I oto kolega przysłał zdjęcie (4) z podpisem „Oto felga z Bielska”. Ciekawy wzór, prawda? Wszystko, co jest pięciokątne, jest ładne. Jaką geometrię można tu zobaczyć? Zacząłem od przerobienia tego deseniu na bardziej geometryczny - w sensie szkolnej geometrii, gdzie mamy jednak proste figury. Wyszło coś takiego - jak na rysunku 5.
W szkole uczymy (się albo innych), jak rozwiązywać zadania. Wiele razy dawałem i uczniom, i nauczycielom, zagadnienie odwrotne: ułożyć zadanie na jakiś temat. Zawsze szło opornie. Nic dziwnego: O dostrzeganiu problemów, stawianiu zagadnień i inteligentnemu przypatrywaniu się światu nie mówi się w szkole prawie wcale. „Czy umiecie się dziwić?” - taki był tytuł książki wydanej dawno temu przez redakcję miesięcznika naukowego „Delta”.
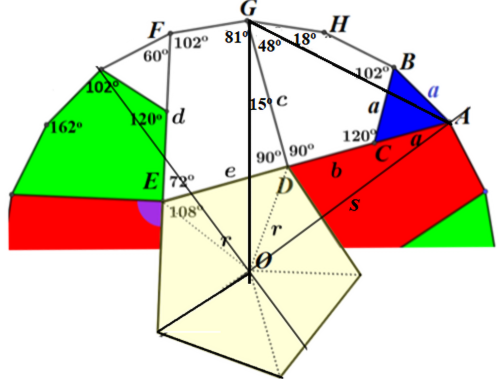
Na „feldze z Bielska” zobaczyłem pięć dziobów ptasich. Przerobiłem ornament na geometrycznie prostszy. Oj, czy naprawdę prosty - to się okaże. Na rysunku 5 dziobom odpowiadają czerwone czworokąty z przyczepionymi niebieskimi trójkątami. Budowę figury zacząłem właśnie od narysowania pięciu trójkątów równobocznych w dwudziestokącie. Długość boku trójkątów oznaczyłem przez a. I oto główne Zadanie 1. Przyjmując, że bok niebieskiego trójkąta równobocznego ma długość a, obliczyć wszystkie kąty i wszystkie rozmiary figur tam widocznych.
Ponieważ zrobienie rysunku zajęło mi kilkanaście minut, to pomyślałem sobie, że obliczenia potrwają może trzy razy tyle, może cztery, może aż godzinę. Hm, nie powiem, ile siedziałem nad tym zadaniem. Zobaczmy. Już rachunek kątów zadziwia. Takich kątów nie spotyka się na szkolnych lekcjach. Idźmy systematycznie, bo się przyda. Przypomnijmy sobie lekcję geometrii.
Nietrudno wyznaczyć miarę kąta wewnętrznego n-kąta foremnego. Opuszczę naprawdę proste wyprowadzenie, podam tylko końcowy wzór. Kąt w n-kącie foremnym ma miarę

To szkolny materiał. Sprawdźmy tylko, że się zgadza. Dla kwadratu (n=4) istotnie dostajemy 90°, a dla trójkąta równobocznego (n=3) też wyjdzie, jak powinno, 60°. Pięciokąt foremny ma 108°, sześciokąt 120°, dwunastokąt 150°, a dla dwudziestokąta otrzymujemy 162°. W mojej prywatnej, nie całkiem poważnej numerologii kojarzę to z autobusem linii 162 w Warszawie - jeździłem nim na zajęcia uniwersyteckie. Ojej, przepraszam za dygresję.
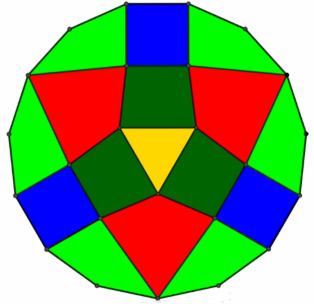
Przypominam, że jedyną daną liczbową w tym zadaniu jest długość boku trójkąta równobocznego. Można powiedzieć, że są jeszcze dwie ważne inne liczby: n=20 (dwudziestokąt), że zaczynamy od trójkątów (a więc m=3) i że jest ich pięć (k=5). Dlatego nazwałem tę felgę F(20, 3, 5). Aby wprawić się w dobry nastrój (i dać sobie serię zadań), narysowałem kilka innych felg. Prawda, że ładne? Na rysunku 7 mamy niezbyt ciekawą konfigurację” sześć trójkątów w sześciokącie. Na rysunku 8 mamy ośmiokąt, trójkąty równoboczne w liczbie 4, a więc jest to F(8,3,4). I tak dalej.
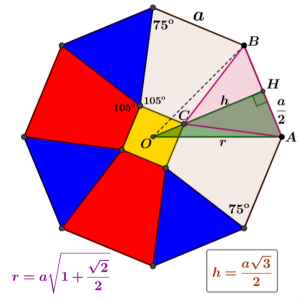
Zadanie 2. Narysuj F(15, 3, 5) i F(15, 5, 3). Potrzebna nam teraz będzie ciekawa i historycznie ważna zależność między długościami boków n-kąta foremnego i 2n-kąta. Spójrzmy na rysunek 12.
Odcinek AC symbolizuje bok n-kąta, a odcinki AB i BC to boki wielokąta o dwa razy większej liczbie boków - tak, że
Wielokąty te są wpisane w okrąg o promieniu r. Chcemy wyznaczyć związek między h i d. Możemy założyć, że promień r jest równy 1, bo związek, którego szukamy, nie może zależeć od promienia okręgu opisanego na tych wielokątach.
Trójkąt ODC (12) jest prostokątny, a więc OD²+DC²=OC², czyli
zatem
Trójkąt BDC też jest prostokątny, a więc BD²+DC²=BC², czyli
Pamiętamy, że
Stąd nasz końcowy wzór
Przyjrzyjmy mu się i wyprowadźmy kilka zależności. Bok kwadratu opisanego na okręgu o promieniu 1 ma długość √2. Dla wielokątów o 8, 16, 32 i 64, … bokach otrzymamy estetycznie wyglądające wzory
i tak dalej.
Przypomnę, że niewymierna liczba π wyraża stosunek obwodu koła do jego średnicy, a to oznaczenie pochodzi od pierwszej litery słowa greckiego oznaczającego obwód (w zlatynizowanej formie perimeter). W starszych źródłach liczba π jest nazywana ludolfiną. Oto dlaczego. Ponad 400 lat temu (w roku 1610) uczony holenderski Ludolph van Ceulen wykorzystał to „i tak dalej”, które było przed chwilą do obliczenia liczby π z dokładnością do 35 cyfr po przecinku. Obliczał kilka lat (!), z pomocą żony. Podwajał liczby boków, obliczał obwody wielokątów i tak zbliżał się do obwodu koła. Doszedł aż do wielokąta foremnego o 262 bokach. Czy możemy sobie wyobrazić taki wielokąt? Zapewne tak. Trudniej wyobrazić sobie, jak daleko odstaje on od okręgu. Zatoczmy w wyobraźni okrąg o promieniu równym odległości Ziemi od najdalszej znanej obecnie galaktyki. Jest nią odkryta w kwietniu 2022 roku galaktyka o o prozaicznym oznaczeniu HD1. Jest od nas odległa o 13,5 miliarda lat świetlnych i jest to najdalszy zaobserwowany od nas obiekt. Wpiszmy w taki okrąg wielokąt foremny o 262 bokach. Jak daleko będzie od odstawać od tego okręgu? Odpowiedź może zdumiewać: o około 20 nanometrów, czyli 20 milionowych części milimetra.
Zadanie 3. Jakie przybliżenie liczby π dostaniemy, gdy użyjemy wielokąta foremnego o 1024 bokach?
Rozwiązanie. Połowa obwodu wielokąta foremnego o tej liczbie boków, wpisanego w okrąg o promieniu 1 jest równa 29·d1024, czyli
Aby obliczyć przybliżoną wartość tego wyrażenia, skorzystałem z popularnego już programu obliczeniowego Wolfram-Alpha. Z dokładnością do pięciu cyfr po przecinku wynikiem jest 3,14159, co jest zgodne z π ≈ 3,14159...
Zadanie 5. Oblicz bok żółtego, środkowego kwadratu dla felgi F(8,3,4). Wskazówka, Spójrz na rysunku 13.
Wracamy do głównego zadania (nr 1): wyznaczeniu rozmiarów figur w „feldze z Bielska”. Skupię się na głównym: obliczeniu boku środkowego, żółtego pięciokąta w środku, (5, 6). Do roboty!
Wychodząc od pięciokąta i podwajając liczbę boków, możemy obliczyć, że
Jest to długość boku niebieskich trójkątów (5, 14), czyli a.
Obliczamy stąd s=OA w zależności od a:
Trójkąt GOA ma kąt przy wierzchołku 540. Stąd możemy wyznaczyć długość odcinka AG. Potrzebujemy do tego wartości sinusa 27°.
Otóż
Jak to obliczyłem? To trochę niewłaściwe pytanie - o tym przy końcu artykułu.
Mamy zatem
co po nieco zawiłych rachunkach znacznie się upraszcza:
Można do tego wzoru dojść prościej, wykorzystując elementy geometrii analitycznej. Ale chcę trzymać się jak najbliżej matematyki szkolnej. Trójkąt GDA wydaje się prostokątny, ale nie jest, choć różnica jest niewielka. Kąt DGA ma 48°, zatem kąt GAD to 42°. Zatem AD=AG sin 48°. Potrzebujemy wartości sin 48°. Oto i ona
Znając AD i kąty trójkąta DOA, możemy z twierdzenia sinusów obliczyć OD=r. Potrzebne są jeszcze wartości sinusów kątów 21° i 36°. Otóż mamy:
I tu „poległem”. Próbowałem napisać końcowy wzór, wyrażający r w zależności od a. To tylko kwestia cierpliwości i kaligrafii, bo przecież „wszystko wyznaczone mam” (jak w piosence, która jest mottem artykułu). Ale czy to ważne? Dla praktycznej konstrukcji nie bardzo.
***
Uff. Ciekawe, czy ktoś doczytał do końca. Mam jakiś dziwny sentyment do skomplikowanych, ale ładnie wyglądający wzorów. Ale w matematyce (przecież i w życiu) ważne jest też spojrzenie ogólne, z jakiejś perspektywy, dystansu na wszystko, co robimy. Spójrzmy zatem i na felgę z Bielska (mowa o Bielsku-Białej na Śląsku; przypomnę, że w czasach zaborów Bielsko należało do Prus, a Biała do Austrii, stąd dzisiejsza podwójna nazwa miasta).
Zobaczmy, że miary wszystkich kątów są podzielne przez 3. To dlatego umiemy podać dokładne wartości ich funkcji trygonometrycznych. Wprawny „trygonometrysta” zrozumie, dlaczego. Na potrzeby zadania o feldze nie obliczałem tych wartości, jak bym to czynił 60 lat temu w szkole - kliknąłem tylko razy klawiaturę. Co więcej, wszystkie takie kąty są konstruowalne za pomocą cyrkla i linijki - a inne kąty o całkowitej liczbie stopni już nie. Dlatego możemy skonstruować pięciokąt, sześciokąt, piętnastokąt, 99-kąt i 102-kąt foremny, a siedmiokąta (foremnego) już nie. Oczywiście możemy go narysować dowolnie dokładnie, odmierzając starannie kąty kątomierzem, ale nie jest to konstrukcja w sensie klasycznej geometrii. Łatwo dają sobie z tym radę najprostsze programy graficzne (w tym i popularna w szkole Geogebra).
Karl Friedrich Gauss (1777–1855, zwany potem „księciem matematyków”) odkrył, jak skonstruować za pomocą cyrkla i linijki 17-kąt foremny i podobno tak się zachwycił swoim odkryciem, że poświęcił się matematyce. Miał wtedy 19 lat. Konstrukcja jest zresztą pomysłowa i oparta na specjalnym „porządku Gaussa” liczb od 0 do 16.
Zadania konstrukcyjne (na budowanie figur za pomocą cyrkla i linijki) były obecne od początku istnienia gimnazjów i liceów i bardzo ważne w szkolnej matematyce. Pochodziły zresztą aż z antyku. Miały wiele zalet: uczyły myślenia i algorytmów, a do pewnego stopnia i sprawności rachunkowej, co było chyba widać. Z grubsza rzecz biorąc, konstruowalne jest to, co da się wyrazić za pomocą pierwiastków kwadratowych. Dzisiaj, jeżeli nawet uczymy myślenia w szkole (a są co do tego różne zdania), to na innych przykładach i innych zadaniach. Problemy konstrukcji za pomocą cyrkla i linijki odeszły w zapomnienie. Trochę żal, jak wszystkiego co było dobre, ale zostało przykryte czymś świeższym.
Michał Szurek