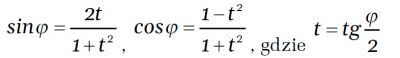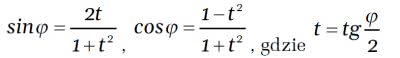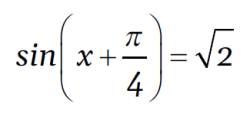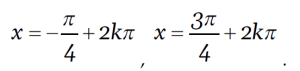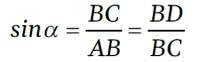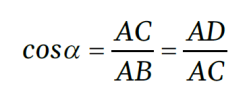Apolonia Inteligentna. Magiczny kafelek

Od pewnego czasu dyskutuje się w mediach o pani Apolonii Inteligentnej - tak na własny użytek nazwałem AI, artificial intelligence, czyli po polsku sztuczną inteligencję. Wciąż jeszcze łatwo ją oszukać, wpisując tak zwane głupie pytania. Nie cieszmy się: Ona się uczy, a na pewno ma utajnione wersje, które już potrafią odpowiedzieć na pytanie filozoficzne, które pozwolę sobie przytoczyć. Pewien kawaler, starający się o rękę panny, został pouczony, że należy trochę porozmawiać o rodzinie, uczuciach i trochę pofilozofować. Na pytanie, czy ma brata, odpowiedziała, że nie. Na pytanie, czy lubi makaron, też odpowiedziała przecząco i konwersacja utknęła, ale konkurent znalazł sposób, by kontynuować i przejść do ogólnych zagadnień o życiu. "Słuchaj, a gdybyś miała brata, to czy on by lubił makaron?"

Takie mam złośliwości w stosunku do pani Apolonii. Ale konkretnie i matematycznie. Dałem jej zadanie, do którego mam duży sentyment. Dostałem je 59 lat temu (!) na egzaminie wstępnym (ustnym) na Uniwersytet Warszawski, na Wydział Matematyki i Fizyki. Na szczęście zorientowałem się od razu, że jest to pytanie podchwytliwe i trochę też dlatego dostałem piątkę z odpowiedzi. Szóstek wtedy nie było. Równanie do rozwiązania było: sinx+cosx=2.

Aby zobaczyć, że równanie to nie ma rozwiązań, wystarczy pamiętać, że obie funkcje są ograniczone przez –1 i 1 oraz, że sinus i cosinus nie mogą być jednocześnie równe 1. A to wynika na przykład z tak zwanej jedynki trygonometrycznej. Z bardzo niewielu informacji matematycznych, jakie większości ludzi zostaje w głowach po ukończeniu szkoły ponadpodstawowej, jest właśnie to, że sin2x+cos2x=1.

Co jednak jest w tym "podchwytliwego?" Otóż w moich szkolnych czasach połowę czasu w klasie X (przedmaturalnej) zajmowała trygonometria, a tu z kolei nacisk położony był na tożsamości i równania. Musieliśmy na pamięć znać wiele wzorów i tożsamości, na przykład na sin(α+β), cos(α+β), sinα+sinβ, a także i ważne podstawienie wymierne, gdzie kluczową rolę gra tangens połowy kąta: 

Tak się zachowała i Apolonia. Poszła w przekształcenia. Komputery lubią obliczenia. Zastosowała prawidłowo wzór na sumę sinusa i cosinusa: 

Otrzymała stąd równanie 

i nie przejmowała się tym, że prawa strona jest większa od 1, tylko znalazła "rozwiązanie"

Widać z tego, że "coś jej się pomieszało" i zamiast √2 po prawej stronie wzięła sobie zero.

***

Zanim jednak zaczniemy wyśmiewać "bezmózgową" Apolonię, spójrzmy, jak sobie poradziła z ciekawym zadaniem o ciągu geometrycznym (cytuję z własnej książki Spacery matematyczne). Wpisałem jej w stosowne okienko:

Była wioska nad rzeką i siedmiu wieśniaków.
Każdy miał siedmiu synów - odważnych chłopaków.
Każdy chłopak posiadał aż siedem kajaków,
A w każdym tym kajaku miał siedem plecaków.
Każdy plecak pomieścić mógł siedem szczupaków
Można złowić szczupaka na siedem robaków. Ile tego jest razem? Robaków, szczupaków,
Plecaków, kajaków, chłopaków, wieśniaków? Wskazówka: miejscowością tą wcale nie był Kraków!

Oto jak rozwiązała to  zadanie pani Apolonia Inteligentna. Kopiuję odpowiedź. 

 ***

Czy to nie przerażające? W licznych rozmowach i artykułach o AI można właśnie wyczuć nutkę strachu: już wkrótce opanują nas sztuczne mózgi. Potem dojdą do wniosku, że należy nas (ludzi) eksterminować i po prostu zabiją. Zanim my wyłączymy im wtyczkę do prądu, one odetną nas od tlenu. Przez krótki czas panice uległem i ja - stwierdziłem po prostu, że sztuczną inteligencją już posługują się studenci na egzaminach i kolokwiach. Sami czynili to jednak niezbyt inteligentnie - od razu było widać, co i jak. Późniejsze dopytywanie ustne potwierdziło, że nie mają pojęcia tym, co piszą i że nie rozumieją, o co chodzi. Nie rozumieją naszym ludzkim umysłem.

Chyba każdy wielki wynalazek wywoływał podobne obawy: od maszyny parowej przez kolej żelazną do komputerów. Kto w dzisiejszej szkole uczy takich technik obliczeniowych, jak próba dziewiątkowa, "dodawanie metodą księgowych", szybkie podnoszenie do kwadratu, pisemne wyciągnie pierwiastka, sprowadzanie do postaci logarytmicznej? To wszystko odeszło w zapomnienie. Szkoda? Tak samo, jak szkoda koni dorożkarskich, lamp naftowych i pisania piórem ze stalówką, maczaną w kałamarzu z atramentem (a kleksy suszyło się bibułą).

Wiemy, że ilość nagromadzonej wiedzy rośnie gwałtownie i "końca nie widać". Jak jednak zauważył Ryszard Kapuściński, najwyraźniej przybywa jej tylko w pamięci komputerów, niekoniecznie w umysłach ludzi. Co gorsza, nie mądrzejemy od tego. Ale to już inna działka.

***

Wynalazkiem, który wciąż ma więcej dobrego niż złego, jest Internet (przewidziany już siedemdziesiąt lat temu przez Stanisława Lema, w książce Powrót z gwiazd, 1963). Ciekawe, że mamy go pisać dużą literą. Dlaczego? Z szacunku? No, to też inny temat. Możemy dzięki niemu (Niemu?) dowiedzieć się wiele i przeczytać opinie powszechnie szanowanych osób na wiele tematów. Niestety, jesteśmy też zasypywani bzdurnymi informacjami, zwykle podawanymi jako "sensacyjne" (pod Piotrkowem urodziło się cielę dwóch głowach, a w Mławie motocyklista Michał wpadł na słup). I najgorsze: trudno nam odróżnić opinię mądrych ludzi od głupich wypowiedzi, albo celowo spreparowanych fake newsów. Trudno zachować dyscyplinę umysłową.

***

O właśnie, wrócę do trygonometrii. Około Świąt Wielkanocnych moja komórka uparcie wyświetlała mi informację, że w matematyce zostało zauważone coś, co czekało 2000 lat na odkrycie. Zrobiłem wyjątek od zasady, że nigdy takich sensacji nie czytam. No i pożałowałem decyzji. Oto bowiem zostałem poinformowany, że Calcea Rujean Johnson i Ne’ Kiya Jackson z Nowego Orleanu udowodniły twierdzenie Pitagorasa za pomocą trygonometrii, ale nie korzystając z "jedynki trygonometrycznej", czyli właśnie z tego, że sin²x+cos²x=1.

"Najwięksi matematycy od ponad 2000 lat próbowali to osiągnąć. Do tej pory opublikowano co najmniej 118 dowodów tego twierdzenia, a Carl Friedrich Gauss wykazał, że tych dowodów jest nieskończenie wiele" - tak napisano na odpowiedniej stronie internetowej, co bezmyślnie przedrukował Focus a powtórzył XY, autor notatki w Internecie. W USA sprawa może ma jeszcze bardziej medialne znaczenie, bo obie dziewczyny-licealistki są czarnoskóre (nie wiem, jak w dobie poprawności politycznej teraz mam nazywać osoby, które… istotnie… są czarnoskóre?).

Najpierw sprawy oczywiście bzdurne. Trygonometria powstała w dobie wczesnego renesansu - w związku z potrzebami praktycznymi, najpierw na potrzeby nawigacji oceanicznej. Dlatego przed znaną nam ze szkoły trygonometrii płaskiej była prawie zapomniana już dzisiaj trygonometria sferyczna. Zauważmy, że gdy w grę wchodzą duże odległości, geometria na powierzchni kuli różni się od tej na płaszczyźnie. Na przykład suma kątów trójkąta, którego jeden wierzchołek jest na biegunie, a dwa na równiku, jest większa od 180 stopni.

Trygonometria miała wielkie znaczenie w pomiarach Ziemi aż do upowszechnienia się nawigacji satelitarnej. Jeszcze pół wieku temu Polska była pokryta siecią drewnianych wież triangulacyjnych. Na Podhalu miały one nawet "ludową" nazwę: patryja. Teraz zamiast nich stoją maszty telefonii komórkowej… Tak czy owak, żadne zadanie o trygonometrii nie może mieć 2000 lat, bo wtedy jej nie było.

"Opublikowano co najmniej 118 dowodów twierdzenia Pitagorasa". Matematycznie, zgadza się. Takie jest znaczenie zwrotu "co najmniej". Gdybym napisał, że "opublikowano co najmniej 500" - też by się zgadzało. Co do rewelacji Gaussa, że dowodów jest nieskończenie wiele - Gauss tego na pewno nie napisał. Pewne jest jednak, że każde twierdzenie można udowodnić jednak na nieskończenie wiele sposobów. To mniej więcej tak, jakby powiedzieć, że do mojego lokalnego sklepiku też mogę dojść na nieskończenie wiele sposób: mogę na przykład dojść tam, idąc przez Lizbonę i Władywostok, za każdym razem inaczej stawiając nogi.

To wszystko jednak "dałoby się znieść", ale nie rewelację, że można użyć trygonometrii, lecz bez jedynki trygonometrycznej. Istotnie, w banalny sposób można stwierdzić, że  owa tożsamość trygonometryczna jest po prostu innym sformułowanie twierdzenia Pitagorasa. Przypomnę, że głosi ono: w trójkącie prostokątnym suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej.

Dowód twierdzenia Pitagorasa za pomocą trygonometrii (bez "jedynki") robimy tak. Bierzemy dowolny dowód i przerabiamy go na trygonometryczny bez użycia "jedynki". Brzmi to trochę tak, jak przepis Juliana Tuwima: jak zrobić esklop? - wziąć pół funta cielęciny, wstrząsnąć i zrobić esklop. No, ale proszę. Wezmę tak zwany dowód Garfielda (XX prezydenta USA, 1831–1881, tak jest, tacy bywali niegdyś prezydenci).

Dowód twierdzenia Pitagorasa "za pomocą" trygonometrii. Jeżeli przypomnimy sobie określenie funkcji podstawowej funkcji trygonometrycznej: sinusa, to zobaczymy, że na rysunku 1 mamy: 

Pierwsza z  tych równości pochodzi z dużego trójkąta ABC, druga z tego "mniejszego" po prawej, czyli BCD. Mamy więc

(*) BC² = AB · DB

Teraz będzie trudniej, bo do gry wejdzie cosinus. Nie ma rady, musimy sobie przypomnieć, co to za funkcja. Zakładam, że Czytelnicy doskonale z tym sobieradzą. Mamy

Pierwsza z tych równości pochodzi, jak poprzednio, z dużego trójkąta ABC, druga z tego mniejszego po lewej, czyli ACD. Mamy więc

(**) AC² = AB · AD

Dodajemy równości oznaczone gwiazdkami: AC²+BC²=AB·AD+AB·DB.

Wyłączamy po prawej stronie AB przed nawias i uwzględniamy to, że AD+DB=AB i mamy twierdzenie Pitagorasa. Korzystałem tylko z tego, czym jest sinus i cosinus.

***

Nic dziwnego, że z dużą podejrzliwością odniosłem się do innej "rewelacji" zamieszczonej przez Forum, że jakoby po 50 latach pracy odkryto świętego Graala matematyki - kształt, którym można pokryć płaszczyznę bez powtarzania wzoru. Dla matematyków to istotnie ciekawe, ale nazywanie tego "świętym Graalem" jest po prostu niesmaczne. Nie jest też tak, że matematycy przez pół wieku tylko szukali jednego kafelka.

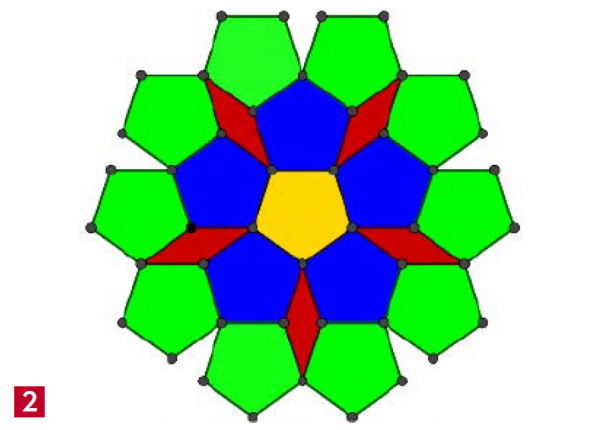
O co chodzi? Jeżeli układamy parkietaż z płytek regularnych kształtach, to wzór prędzej czy później musi się powtórzyć albo mieć jakąś symetrię. Spójrzmy na rysunek 2. Jest zbudowany bardzo regularnie. Układamy obok siebie pięciokąty foremne. Powstaje siatka z oczkami - są nimi brązowe romby. Bardzo estetyczny deseń, prawda? Z matematycznego punktu widzenia jest on okresowy - nie zmienia się przy przesunięciach.

Pytanie, czy są takie parkietaże nieokresowe, postawił w 1961 roku amerykański matematyk chińskiego pochodzenia, Hao Wang, pracujący zresztą w Bell Laboratories. Ale zagadnienie przyszło z  logiki matematycznej - teorii funkcji rekursywnych. Zajmował się nimi między innymi wybitny matematyk polski, Andrzej Mostowski (1913–1975). Przytoczę nawet dane odpowiedniego artykułu: Mostowski, A., A formula with no recursively enumerable model, Fundamenta Mathematicae, vol. 43 (1955), pp. 125–140.

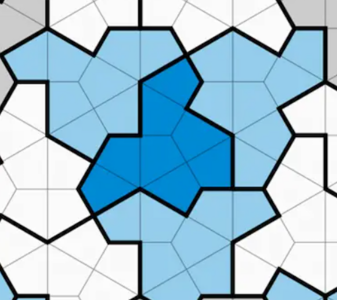
Fakt, że można pokryć płaszczyznę w sposób nieokresowy udowodnił w 1966 r. Robert Berger. Podał on też stosowną konstrukcję, ale jego parkietaż zawierał aż 20 426 kafelków różnych kształtów. Potem redukowano liczbę potrzebnych kafelków (w rozważaniach przydawały się idee maszyny Turinga) aż do osiągnięcia prostego parkietażu Penrose’a, który wymaga tylko dwóch kształtów. To istotnie było pół wieku temu, w 1973 roku. Obecnie wykazano, że wystarczy jeden wielokąt, jeden kształt. Bo choć informację o tym odkryciu zamieszczono w sieci podejrzanie blisko 1 kwietnia, to jednak wydaje się prawdziwa. Trudno przewidzieć, czy i jakie zastosowanie będzie miało to odkrycie. Kafelki Penrose’a posłużyły do opisu kwazikryształów. Podejrzewam, że zgodnie ze współczesnymi trendami ten jeden kafelek może mieć znaczenie w kryptografii. 

3. Kafelki Penrose’a (źródło: Wikipedia, hasło: kafelki Penrose’a)

4. Trzynastokąt do nieokresowego wypełnienia płaszczyzny

Michał Szurek