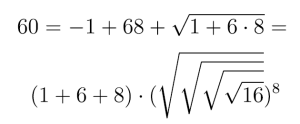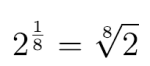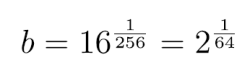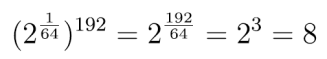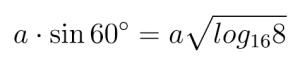O dwóch liczbach, które się lubią

Nie trzeba się wiele znać na matematyce, by się zgodzić, że cokolwiek to znaczy, to najprostszą symetrią (a więc „atomem wodoru”) musi być ta, z którą spotykamy się codziennie już od samego rana: Czytelnicy przy goleniu, Czytelniczki przy makijażu. To symetria lustrzana, lewo i prawo, łacińska litera R i pochodząca z cyrylicy Я, ale także plus i minus, góra i dół, dobro i zło, orientalne ying i yang i tak dalej, i tak dalej. Jakie są inne „atomy symetrii”? W ich poszukiwaniu pewną rolę grają dwie liczby: 60 i 168. No i właśnie, dziś będzie tylko o tych liczbach - raczej ciekawostki, ale z bardziej poważną nutką: te liczby lubią się na-wzajem, lubią stać obok siebie. Także przy poszukiwaniu symetrii. O tym za miesiąc.

***

Zacznę od zabawy, którą sam uważam za niezbyt mądrą, ale… gdy jestem na  nudnych zebraniach, to zamiast rysować kwiatki, bawię się właśnie tak. W wersji na dzisiaj: czy da się wyrazić liczbę 60 za pomocą cyfr 1, 6, 8, użytych w tej właśnie kolej-ności, połączonych dowolnymi znakami arytmetycz-nymi. Można powtórzyć sekwencję 1, 6, 8 - ale nie można żadnej cyfry opuścić.

Przy jednokrotnym użyciu 1, 6, 8 chyba nie da się otrzymać 60, ale z dwóch „168” już można złożyć sześćdziesiątkę i to na kilka sposobów:

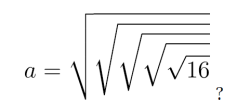
Zabawa ma mimo wszystko pewien walor dydaktyczny: uczy „wyobraźni liczbowej”. Dorzucę we wzorze jeszcze jeden pierwiastek. Oto powtórka przed egzaminem maturalnym. Ile jest równy logarytm 8 przy podstawie

Obliczmy! Wspomnę tu swoje szkolne czasy, kiedy musieliśmy recytować bez zająknięcia formułkę: logarytm liczby a przy podstawie p jest to wykładnik potęgi, do której należy podnieść podstawę, aby otrzymać liczbę logarytmowaną a.

Obliczajmy zatem, ile to jest 

Liczba 16 to 2⁴, a wyciąganie pierwiastka to podnoszenie do potęgi , a więc

Do której potęgi trzeba podnieść

żeby dostać 8=2³? To proste: do potęgi 24. Zgadzacie się, maturzyści „wiosna 24”? Szukany logarytm to 24.

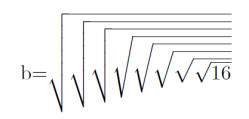
Ćwiczmy wobec tego dalej rachunki na potęgach i logarytmach. Niech

Wygląda trochę obłędnie, to prawda. No to ile jest równy logarytm liczby 8 przy tej podstawie b? Jedyna trudność to  policzyć, ile jest znaków pierwiastka. Jest ich osiem, a zatem

Do której potęgi trzeba podnieść tę liczbę, żeby otrzymać 8? Oczywiście do 192, bo przecież:

Zabawa robi się skomplikowana. Mamy oto jeszcze jeden sposób przedstawienia liczby 60 za pomocą dwukrotnego użycia jedynki, szóstki i ósemki (i symboli działań arytmetycznych):

Owszem, to trochę „z lekka bez sensu”, ale wiele zabaw jest takich. Na pewno jest lepsza niż strzelanie do statków kosmicznych albo do potworów w telefonie komórkowym.

***

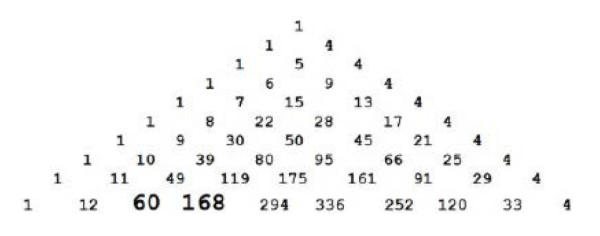
Liczby 60 i 168 lubią stać koło siebie. Oto pierwszy przykład. Większość Czytelników wie, jaka jest zasada budowy tak zwanego trójkąta Pascala: każda liczba jest sumą dwóch stojących nad nią. Oczywiście z wyjątkiem liczb na skraju trójkąta - one nie mają nad sobą dwu innych. W zwykłym trójkącie Pascala boki są złożone z jedynek. W napisanym dalej lewy bok składa się z jedynek, prawy z czwórek. Zasada pozostaje bez zmian: każda liczba jest sumą dwóch stojących nad nią. W najniższym rzędzie poniższego diagramu mamy nasze liczby, 60 i 168, obok siebie.

***

Ile rozwiązań w liczbach całkowitych ma równanie x²+y²+2z²+6t²=62? Można wyliczyć, że 60. Zamieńmy 62 po prawej stronie tego równania na liczbę o jeden większą: 63. Ile będzie rozwiązań? Jest ich 168, kto nie wierzy, niech sprawdzi. To proste zadanie z programowania, a Apolonia Inteligentna (AI) sama ułożyła mi odpowiedni program w języku Python. Potem tylko nacisnąłem Run i program się wykonał. Nie musiałbym nawet znać tego pytona. Apolonią nazywam tu Sztuczną Inteligencję, którą niektórzy byliby skłonni nawet nazywać Antychrystem.

Muszę jednak przyznać, że po rozwiązaniu tego zadania zrobiło mi się trochę gorzko. Nauka programowania (najpierw w BASIC-u, potem w TurboPascalu, wreszcie w języku Mathematica) zajęła mi kiedyś tygodnie, a nawet miesiące pracy. Teraz nie musiałem nawet myśleć - „ona” wszystko zrobiła. Ale to tak już jest i musi być. 60 lat temu przedzierałem się przez śliczną i dziką dolinę w Gorcach - nawet z pewnym strachem, bo samotnie. Bez ścieżki, wzdłuż potoku.

Dziś biegnie tam wygodna droga leśna, a przewodniki określają wycieczkę jako nudną i uciążliwą. Ilekroć coś zyskujemy, coś także tracimy. Nie można jednak wracać do króla Ćwieczka. A że czasem żal?

Po  dłuższej chwili wrócił mi lepszy humor. Sztuczna Inteligencja (przynajmniej w wersji ogólnodostępnej) robi tak dużo błędów, że nie można jej wierzyć. Trzeba sprawdzać, sprawdzać i sprawdzać. Tak też i ja musiałem zrobić - zweryfikować, czy aby naprawdę napisała, co powinna była napisać. Do tego już była potrzebna moja ludzka wiedza. Komputer oblicza i  udaje, że myśli. Człowiek myśli naprawdę. Za życia moich dzieci jeszcze to się nie zmieni - być może wnuki będą mieć z tym problem. Wróćmy na bezpieczne wody, to jest do matematyki.

***

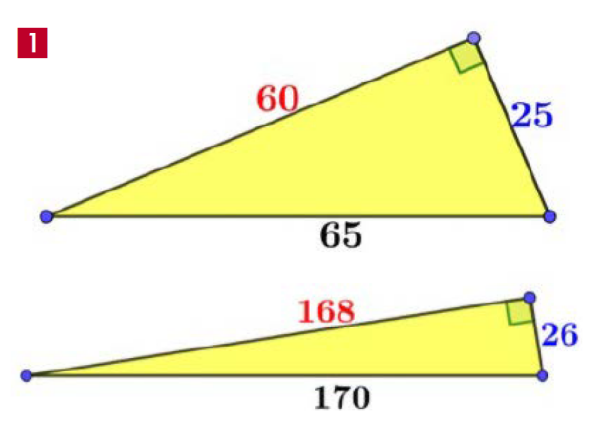
Oto i następny przykład, że 60 i 168 lgną do siebie. Trójką pitagorejską nazywamy trzy liczby naturalne, które mogą być długościami boków trójkąta prostokątnego. Pierwszym, najprostszym przykładem jest tak zwany trójkąt egipski: 3, 4, 5. Podobno Egipcjanie używali go do wyznaczania kąta prostego. Czy znajdzie się trójka pitagorejska, w której najmniejszą liczbą jest 25? Tak, znajdzie się - najmniejsza z nich to (25, 60, 65). Sprawdźmy: 25²+60²=65². Trójkąt o tych bokach jest prostokątny.

Zwiększmy liczbę o 1, czyli zamieńmy 25 na 26. Czy znajdzie się trójka pitagorejska, w której najmniejszą liczbą jest 26? Tak, znajdzie się - najmniejsza z nich to (26, 168, 170). Sprawdźmy: 25²+60²=65² (rysunek 1). Trójkąty są narysowane w różnej skali, dlatego 26 wydaje się trzy razy krótsze niż 25.

***

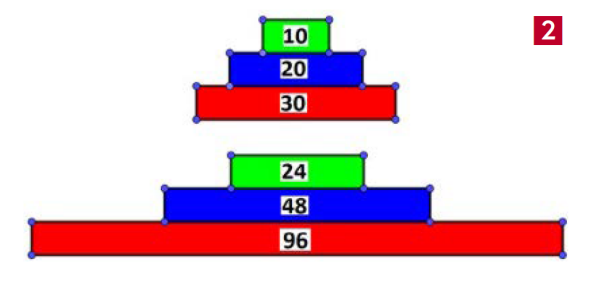
Na rysunku 2 widzimy inną koligację. Liczba 60 jest przedstawiona jako suma trzech liczb tworzących ciąg arytmetyczny: 30+20+10, a liczba 168 jako sumę trzech liczb w ciągu geometrycznym: 96+48+24. I taki to Hawrań i Murań z naszych liczb. Skąd mi przyszło do głowy takie skojarzenie? Z wakacji, które spędziłem na Spiszu, w domu z widokiem na Tatry Bielskie. Każdy, kto choć trochę zna Tatry, wie o „parze przyjaciół”: Hawrań i Murań. Góry całkiem do siebie niepodobne, a  jednak coś je spaja, może tylko podobna nazwa? Zawsze są łączone - a nawet nie stoją obok siebie. Oddziela je szpiczasty Nowy Wierch o „matematycznej” wysokości, 1999 m. Chociaż to kącik matematyczny, to trochę poezji nie zaszkodzi.

Przez dolinę z oddali
leśną radość wołali,
a zwabiony wołaniem,
stanął Hawrań z Muraniem,
jak ich dwoje na hali.

(Władysław Broniewski, Hawrań i Murań)

***

Przejdźmy do nieco bardziej zaawansowanej, ale wciąż prostej arytmetyki. Liczby 60 i 168 są też związane funkcją Eulera, to jest sumą dzielników. Zobaczmy, 60 dzieli się przez 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 i 60. Dodajmy:

1+2+3+4+5+6+10+12+15+20+30+60=168.

Suma dzielników liczby 60 jest równa 168. To jest wartość funkcji Eulera dla n=60. Niestety, suma dzielników liczby 168 to 480. Gdyby była „z powrotem” równa 60, to liczby te byłyby „zaprzyjaźnione”, tak się naprawdę nazywają w arytmetyce. Pitagoras mawiał: „przyjaciel to drugi ja, przyjaźń to stosunek liczb 220 i 284”.

Chodzi tu właśnie o to, że suma dzielników liczby 220 jest równa 284, a suma dzielników 284 to 220.

Nieco bardziej skomplikowana reguła wiąże 60 i 168 tak oto. Oznaczmy wspomnianą funkcję Eulera (czyli sumę dzielników liczby n) przez σ(n). Widzieliśmy, że σ(60)=168. Mamy: σ(σ(23))=60, σ(σ(24))=168.

Znów nasze liczby ustawiły się obok siebie. Istotnie, coś do siebie czują…

I jeszcze jedno z dzielnikami, z jeszcze bardziej zaawansowanej teorii liczb. Pół wieku temu (w 1974 roku) Mathukumalli Venkata SubbaRao (matematyk kanadyjski indyjskiego pochodzenia i Enrst Gabor Strauss (Niemcy —> USA) rozważali funkcję, której ogólnego wzoru przytaczać nie będę, bo lepiej wyjaśni to sugestywny przykład. Niech daną liczbą będzie n=360. Rozkładam na czynniki pierwsze:

360=2³∙3²∙5

i tworzę iloczyn

(1+2+2²+2³)(1+3+3²)(1+5)=15∙13∙6=1170

To  jest wartość funkcji SubbaRao-Straussa dla n=360. Dla n=2023=7 17² mielibyśmy (1+7)(1+17+17²)=8∙307=2456, a  dla n=2024=2³∙11∙23 dostaniemy (1+2+2²+2³)(1+11)(1+23)=15∙12∙24=2016.

No i proszę. Dla n=59 mamy 1+59=60, a dla n=60=2²∙3∙5 otrzymujemy

(1+2+2²)∙(1+3)∙(1+5)=7∙4∙6=168

***

Wiemy, że 60 ma wiele wspólnego z zegarem. Dawno temu był w Polskim Radiu satyryczny program „60 minut na godzinę”. Ale 168 też ma coś wspólnego z czasem: tydzień ma 168 godzin.

***

Wysokością trójkąta równobocznego o boku a jest

3. Liczbę 168 mamy i w trójkącie równobocznym

***

Jest 168 liczb pierwszych mniejszych niż 1000. Liczba 168 jest iloczynem dwóch najmniejszych liczb doskonałych, 6 i 28. Liczby doskonałe podobały się już Pitagorasowi i świętemu Augustynowi: to liczby równe sumie swoich dzielników właściwych (to znaczy mniejszych od niej samej):

6=1+2+3, 28=1+2+4+7+14

W niewielu miastach w Polsce jest autobus nr 168. Znalazłem go w Gdańsku, Katowicach, Krakowie, Poznaniu, Warszawie i Wrocławiu. Studiów nad liniami autobusowymi linii 60 nie przeprowadzałem. Zobaczyłem tylko, że kursuje w Gliwicach i nie ma styczności z katowickim 168.

60 lat temu byłem po raz pierwszy na Rysach. Było nas kilkanaście osób. 168 lat temu zmarł Adam Mickiewicz, a także Karol Gauss.

***

Takich zależności można by zapewne znaleźć więcej. To w zasadzie tylko ciekawostki. Zasadniczym celem artykułu miało być zupełnie co innego. Jest 60 permutacji parzystych liczb 1, 2, 3, 4, 5. Każda taka permutacja odpowiada pewnej symetrii dwunastościanu foremnego, a wszystkie razem tworzą tak zwaną grupę alternującą A5. W algebrze jest to najmniejsza nieabelowa grupa prosta. Opowieść o takich grupach (i dlaczego się nimi zajmujemy) wypełni mi odcinek za miesiąc. A gdzie jest w tym 168? Jest to liczba elementów w następnej grupie prostej, związanej z nazwiskiem włoskiego matematyka Gino Fano (1871–1952).

Dopiero kilkanaście lat temu skompletowano listę wszystkich grup prostych. Nie licząc grup „łatwych do zbadania” (dla tych, którzy wiedzą, o co chodzi: grup cyklicznych Zp), lista zaczyna się od grup mających 60 i 168 elementów, a kończy na grupie mającej ich „trochę więcej”, a mianowicie

2⁴⁶∙3²⁰∙5⁹·7⁶∙11²∙13²∙17∙19∙23∙29∙31∙41∙47∙59∙71= 
808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000

Trudno nawet wyobrazić sobie, jak wielka jest to liczba. Tyle elektronów miałoby masę spoczynkową równą (z dobrym przybliżeniem) jednej dziesiątej masy naszego Księżyca. Grupy proste to swego rodzaju „atomy symetrii”, a ich lista to dla matematyka jak tablica Mendelejewa dla chemika. 

Michał Szurek